题目内容
2.对于曲线C所在平面上的定点P0,若存在以点P0为顶点的角α,使得α≥∠AP0B对于曲线C上的任意两个不同的点A,B恒成立,则称角α为曲线C相对于点P0的“界角”,并称其中最小的“界角”为曲线C相对于点P0的“确界角”.曲线C:y=$\sqrt{{x^2}+1}$相对于坐标原点O的“确界角”的大小是$\frac{π}{2}$.分析 画出曲线C:y=$\sqrt{{x^2}+1}$的图象,过点O作出两条直线与曲线无限接近,曲线y=$\sqrt{{x}^{2}+1}$与直线y=k1x、y=k2x无限接近,即为双曲线的渐近线,故k1=1;k2=-1,即可得到所求的“确界角”.
解答 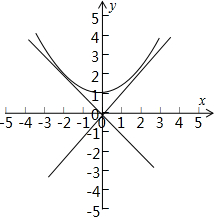 解:画出曲线C:y=$\sqrt{{x^2}+1}$的图象,过点O作出两条直线与曲线无限接近,设它们的方程分别为y=k1x,y=k2x,
解:画出曲线C:y=$\sqrt{{x^2}+1}$的图象,过点O作出两条直线与曲线无限接近,设它们的方程分别为y=k1x,y=k2x,
曲线y=$\sqrt{{x}^{2}+1}$与直线y=k1x、y=k2x无限接近,即为双曲线的渐近线,故k1=1;k2=-1,
故曲线C相对于点O的“确界角”为$\frac{π}{2}$.
故答案为:$\frac{π}{2}$
点评 本题考查新定义“确界角”及应用,考查双曲线的性质:渐近线,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知a>0,b>1且2a+b=4,则$\frac{1}{a}$+$\frac{2}{b-1}$的最小值为( )
| A. | 8 | B. | 4 | C. | 2$\sqrt{2}$ | D. | $\frac{8}{3}$ |
7.执行如图所示的程序框图,若输出的结果为3,则可输入的实数x的值的个数为( )

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.已知随机变量ξ服从正态分布N(2,σ2),且P(ξ<4)=0.8,则P(0<ξ<2)等于( )
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |