题目内容
14.函数$f(x)=1-2{sin^2}(x+\frac{π}{2})$的相邻两个对称中心之间的距离是( )| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
分析 由条件利用二倍角的余弦公式化简函数的解析式,再利用余弦函数的图象的性质得出结论.
解答 解:函数$f(x)=1-2{sin^2}(x+\frac{π}{2})$=cos(2x+π)=-cos2x 的相邻两个对称中心之间的距离为$\frac{T}{2}$=$\frac{π}{2}$,
故选:C.
点评 本题主要考查二倍角的余弦公式、余弦函数的图象的性质,属于基础题.

练习册系列答案
相关题目
9.以直线y+x=0为对称轴且与直线y-3x=2对称的直线方程为( )
| A. | y=$\frac{x}{3}$+$\frac{2}{3}$ | B. | y=-$\frac{x}{3}$+$\frac{2}{3}$ | ||
| C. | y=-3x-2 | D. | y=-3x+2 | ||
| E. | 以上结果均不正确 |
6.已知函数f(x)=$\frac{1}{3}$|sin2πx|,ai=$\frac{i}{19}$(i=0,1,2,…,19),I=|f(a1)-f(a0)|+|f(a2)-f(a1)|+…+|f(a19)-f(a18)|,则( )
| A. | I>1 | B. | I<1 | C. | I=1 | D. | 以上都不对 |
3.直线x=$\frac{1}{2}$,x=2,y=0,及曲线y=$\frac{1}{x}$所围图形的面积为( )
| A. | $\frac{15}{4}$ | B. | $\frac{17}{4}$ | C. | $\frac{1}{2}ln2$ | D. | 2ln2 |
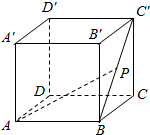 如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.
如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.