题目内容
(本小题满分12分)
甲、乙两名射击运动员,甲射击一次命中10环的概率为 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
, 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及 的分布列, (2)求
的分布列, (2)求 的数学期望.
的数学期望.
甲、乙两名射击运动员,甲射击一次命中10环的概率为
 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ= ,
, 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.(1)求s的值及
 的分布列, (2)求
的分布列, (2)求 的数学期望.
的数学期望.(1) 略(2) 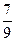
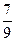
(1)依题意知ξ∽B(2,s),故Eξ=2s= ,∴s=
,∴s=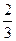 . …………2分
. …………2分
 的取值可以是0,1,2.甲、乙两人命中10环的次数均为0次的概率
的取值可以是0,1,2.甲、乙两人命中10环的次数均为0次的概率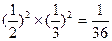 ,甲、乙两人命中10环的次数均为1次的概率是
,甲、乙两人命中10环的次数均为1次的概率是 ,甲、乙两人命中10环的次数均为2次的概率是
,甲、乙两人命中10环的次数均为2次的概率是 ,∴
,∴ (
(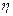 =0)=
=0)= . …………6分
. …………6分
甲命中10环的次数为2次且乙命中10环的次数为0次的概率是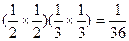 ,甲命中10环的次数为0次且乙命中10环的次数为2次的概率是
,甲命中10环的次数为0次且乙命中10环的次数为2次的概率是 .∴
.∴ (
( =2)=
=2)=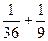 =
= ,
,
∴ (
( =1)=1
=1)=1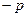 (
( =0)
=0)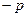 (
( =2)=
=2)= . ………10分
. ………10分
故 的分布列是
的分布列是
………11分
(2)E =
= . …………12分
. …………12分
 ,∴s=
,∴s=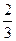 . …………2分
. …………2分 的取值可以是0,1,2.甲、乙两人命中10环的次数均为0次的概率
的取值可以是0,1,2.甲、乙两人命中10环的次数均为0次的概率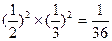 ,甲、乙两人命中10环的次数均为1次的概率是
,甲、乙两人命中10环的次数均为1次的概率是 ,甲、乙两人命中10环的次数均为2次的概率是
,甲、乙两人命中10环的次数均为2次的概率是 ,∴
,∴ (
(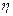 =0)=
=0)= . …………6分
. …………6分甲命中10环的次数为2次且乙命中10环的次数为0次的概率是
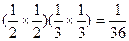 ,甲命中10环的次数为0次且乙命中10环的次数为2次的概率是
,甲命中10环的次数为0次且乙命中10环的次数为2次的概率是 .∴
.∴ (
( =2)=
=2)=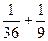 =
= ,
, ∴
 (
( =1)=1
=1)=1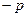 (
( =0)
=0)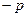 (
( =2)=
=2)= . ………10分
. ………10分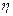 | 0 | 1 | 2 |
 | 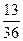 |  |  |
 的分布列是
的分布列是………11分
(2)E
 =
= . …………12分
. …………12分
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 (假定每次通过率相同)
(假定每次通过率相同)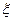 的分布列及数学期望;
的分布列及数学期望; )
)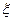 是离散型随机变量,则
是离散型随机变量,则 的值为( )
的值为( )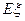
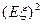
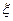 的分布列为:
的分布列为:  ,则
,则 ___,
___, ___.
___. 都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为
都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间是相互独立的,其规律为

