题目内容
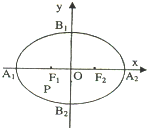 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| A1B1 |
| A1A2 |
为1.
(1)求椭圆C的方程;
(2)是否存在同时满足以下条件的直线:①与椭圆相交于M,N两点,以线段MN为直径的圆过原点;
②与圆心在原点,半径为c的圆相切;若存在,求出直线l的方程;若不存在,请说明理由.
分析:(1)由题设条件,利用向量
在向量
上的投影为2,且椭圆上的点到焦点距离的最小值为1,求出a=2,c=1,由此能求出椭圆方程.
(2)假设满足题设的直线l存在,设M,N两点坐标分别为(x1,y1),(x2,y2),当l不垂直于x轴时,设l方程为y=kx+m,直线与x2+y2=1相切,由题设条件得到不存在这样的实数k,此直线l不存在.当l垂直于x轴时,直线l的方程为x=1或x=-1,推出此直线l也不存在.
| A1B1 |
| A1A2 |
(2)假设满足题设的直线l存在,设M,N两点坐标分别为(x1,y1),(x2,y2),当l不垂直于x轴时,设l方程为y=kx+m,直线与x2+y2=1相切,由题设条件得到不存在这样的实数k,此直线l不存在.当l垂直于x轴时,直线l的方程为x=1或x=-1,推出此直线l也不存在.
解答:解:(1)A1(-a,0),B1(0,b),A2(a,0),
∴
=(a,b),
=(2a,0),
∴
=2=
=a,
∴a=2.(2分)
又a-c=1,∴c=1,
b2=a2-c2=3,
∴椭圆方程为
+
=1.(5分)
(2)假设满足题设的直线l存在,设M,N两点坐标分别为(x1,y1),(x2,y2),
①当l不垂直于x轴时,设l方程为y=kx+m,
直线与x2+y2=1相切,
∴
=1,即m2=k2+1.
又以MN为直径的圆过原点,
∴OM⊥ON,∴x1x2+y1y2=0,(7分)
奖y=kx+m代入椭圆方程,得(3+4k2)x2+8kmx+4m2-12=0,
∴x1+x2=
,x1x2=
,
∴x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
∴(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,
将m2=1+k2代入,得-5(k2+1)=0,即不存在这样的实数k,
∴此直线l不存在.(10分)
②当l垂直于x轴时,直线l的方程为x=1或x=-1,
当x=1时,直线l与椭圆的交点为(1,
)和(1,-
),
•
=1-
≠0.(11分)
当x=-1时,同理,得
•
≠0,即此直线l也不存在.
综上,满足条件的直线l不存在.(13分)
∴
| A1B1 |
| A1A2 |
∴
| ||||
|
|
| 2a2 |
| 2a |
∴a=2.(2分)
又a-c=1,∴c=1,
b2=a2-c2=3,
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)假设满足题设的直线l存在,设M,N两点坐标分别为(x1,y1),(x2,y2),
①当l不垂直于x轴时,设l方程为y=kx+m,
直线与x2+y2=1相切,
∴
| |m| | ||
|
又以MN为直径的圆过原点,
∴OM⊥ON,∴x1x2+y1y2=0,(7分)
奖y=kx+m代入椭圆方程,得(3+4k2)x2+8kmx+4m2-12=0,
∴x1+x2=
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
∴x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=0,
∴(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,
将m2=1+k2代入,得-5(k2+1)=0,即不存在这样的实数k,
∴此直线l不存在.(10分)
②当l垂直于x轴时,直线l的方程为x=1或x=-1,
当x=1时,直线l与椭圆的交点为(1,
| 3 |
| 2 |
| 3 |
| 2 |
| OM |
| ON |
| 9 |
| 4 |
当x=-1时,同理,得
. |
| OM |
| ON |
综上,满足条件的直线l不存在.(13分)
点评:本题考查椭圆方程的求法,判断直线l是否存在.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
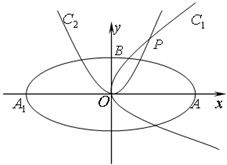 如图,椭圆C:
如图,椭圆C: (2008•闸北区二模)如图,椭圆C:
(2008•闸北区二模)如图,椭圆C: 如图,椭圆
如图,椭圆 如图,椭圆
如图,椭圆 (2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C:
(2011•重庆三模)光线被曲线反射,等效于被曲线在反射点处的切线反射.已知光线从椭圆的一个焦点出发,被椭圆反射后要回到椭圆的另一个焦点;光线从双曲线的一个焦点出发被双曲线反射后的反射光线等效于从另一个焦点发出;如图,椭圆C: