题目内容

已知向量a≠e，| e |＝1，对任意t∈R，恒有|a－t e |≥|a－e |，则

(A) a⊥e      (B) a⊥(a－e)  (C) e⊥(a－e)  (D) (a＋e)⊥(a－e)

C

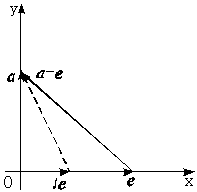
解法一：对于选项A，取a⊥e，如下图所示，易见t在（0，1）取值时，|a－te|<|a－e|，故A不成立.

对于选项B，取a⊥（a－e），如下图所示，易见在（0，1）内存在t使|a－te|<|a－e|，故B不成立.

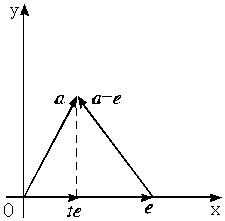
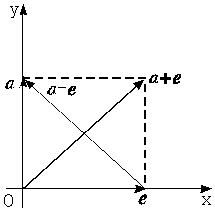
对于选项D，取定a，e使（a+e）⊥（a－e），如下图所示，易见在（0，1）内，无论t取何值，|a－te|<|a－e|，故D不成立.

综合知，C成立.

解法二：∵t∈R，恒有|a－te|≥|a－e|，等价于|a－te|2≥|a－e|2恒成立，即（a－te）2≥（a－e）2恒成立.

展开整理得t2－2a·et+（2a·e－1）≥0对任意t∈R均成立，

则需方程的判别式

Δ=（－2a·e）2－4（2a·e－1）≤0.

整理得（a·e）2－2（a·e）+1≤0，

即（a·e－1）2≤0.∴a·e=1.

∴e·（a－e）=e·a－e2=1－1=0.

∴e⊥（a－e）.故选C.

 

 


练习册系列答案
相关题目
已知向量
a
≠
e
，|
e
|=1，对任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，则（　　）
A、
a
⊥
e
B、
a
⊥（
a
-
e
）
C、
e
⊥（
a
-
e
）
D、（
a
+
e
）⊥（
a
-
e
）
已知向量
a
≠
e
，|
e
|=1，对任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，则（　　）
A、
a
⊥
e
B、
a
⊥（
a
-
e
）
C、
e
⊥（
a
-
e
）
D、（
a
+
e
）⊥（
a
-
e
）
已知向量a≠e,|e|=1满足:对任意t∈R,恒有|a-te|≥|a-e|,则(    )

A.a⊥e            B.a⊥(a-e)             C.e⊥(a-e)              D.(a+e)⊥(a-e)

已知向量a≠e，|e|=1对任意t∈R，恒有|a-te|≥|a-e|，则（    ）

A.a⊥e                                       B.a⊥(a-e)

C.e⊥(a-e)                                 D.(a+e)⊥(a-e)
已知向量
a
≠
e
，|
e
|=1，对任意t∈R，恒有|
a
-t
e
|≥|
a
-
e
|，则（　　）
A．
a
⊥
e
B．
a
⊥（
a
-
e
）		C．
e
⊥（
a
-
e
）		D．（
a
+
e
）⊥（
a
-
e
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网