题目内容
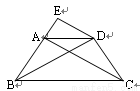
如图,等腰梯形ABCD中,线段Ab的中点O是抛物线的顶点,DA、AB、BC分别与抛物线切于点M、O、N.等腰梯形的高是3,直线CD与抛物线相交于E、F两点,线段EF的长是4.(Ⅰ)建立适当的直角坐标系,求抛物线的方程;
(Ⅱ)求等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.
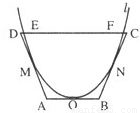
【答案】分析:(Ⅰ)以AB所在直线为x轴,以O为圆点,建立直角坐标系,则F(2,3),设抛物线方程为y=ax2,a>0,将F(2,3)代入,能够求出抛物线方程.
(Ⅱ)由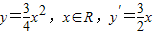 ,设N(x,y),过点N的切线方程为
,设N(x,y),过点N的切线方程为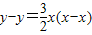 ,令y=0,又
,令y=0,又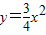 ,
,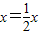 ,由此能求出等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.
,由此能求出等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.
解答:解:(Ⅰ)以AB所在直线为x轴,以O为圆点,建立直角坐标系,则F(2,3),
设抛物线方程为y=ax2,a>0,
将F(2,3)代入,得a= ,
,
所以,抛物线方程为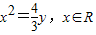 ,
,
(Ⅱ)由(Ⅰ)知: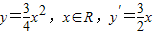 ,
,
设N(x,y),过点N的切线方程为 ,
,
令y=0,又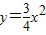 ,∴
,∴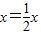 ,
,
∴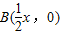 .
.
令y=3,又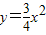 ,∴
,∴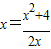 ,
,
∴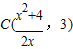 ,
,
∴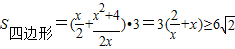 ,
,
当且仅当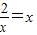 ,即
,即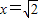 时,取“=”号,此时N(
时,取“=”号,此时N(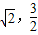 ),M(-
),M(-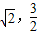 ).
).
点评:本题考查抛物线的性质和应用.解题时要认真审题,仔细解答,注意均值不等式的合理运用.
(Ⅱ)由
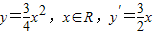 ,设N(x,y),过点N的切线方程为
,设N(x,y),过点N的切线方程为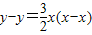 ,令y=0,又
,令y=0,又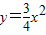 ,
,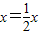 ,由此能求出等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.
,由此能求出等腰梯形ABCD的面积的最小值,并确定此时M、N的位置.解答:解:(Ⅰ)以AB所在直线为x轴,以O为圆点,建立直角坐标系,则F(2,3),
设抛物线方程为y=ax2,a>0,
将F(2,3)代入,得a=
 ,
,所以,抛物线方程为
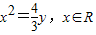 ,
,(Ⅱ)由(Ⅰ)知:
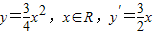 ,
,设N(x,y),过点N的切线方程为
 ,
,令y=0,又
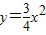 ,∴
,∴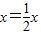 ,
,∴
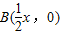 .
.令y=3,又
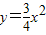 ,∴
,∴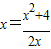 ,
,∴
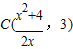 ,
,∴
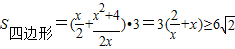 ,
,当且仅当
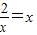 ,即
,即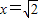 时,取“=”号,此时N(
时,取“=”号,此时N(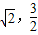 ),M(-
),M(-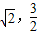 ).
).点评:本题考查抛物线的性质和应用.解题时要认真审题,仔细解答,注意均值不等式的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2
(2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2