题目内容
函数 的单调递减区间( )
的单调递减区间( )
A. | B. |
C. | D. |
C
解析试题分析:原式变形得 ,欲求函数的减区间,即求
,欲求函数的减区间,即求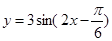 的增区间,又
的增区间,又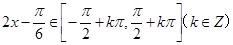 ,解得
,解得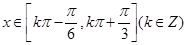 .
.
考点:三角函数的单调性.

练习册系列答案
相关题目
设角 是第二象限角,且
是第二象限角,且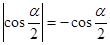 ,则
,则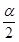 角的终边在( )
角的终边在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
与60°角终边相同的角的集合可以表示为( )
A.{ | | =k·360°+ =k·360°+ ,k ,k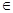 Z} Z} |
B.{ | | =2k =2k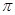 +60°,k +60°,k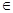 Z} Z} |
C.{ | | =k·180°+60°,k =k·180°+60°,k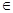 Z} Z} |
D.{ | | =2k =2k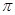 + + ,k ,k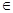 Z} Z} |
将函数 的图象沿
的图象沿 轴向左平移
轴向左平移 个单位后,得到一个关于
个单位后,得到一个关于 轴对称的图象,则
轴对称的图象,则
的一个可能取值为( )
A. | B. | C. | D. |
为了得到函数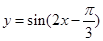 的图像,只需把函数
的图像,只需把函数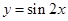 的图像( )
的图像( )
A.向右平移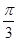 个长度单位 个长度单位 | B.向右平移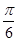 个长度单位 个长度单位 |
C.向左平移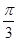 个长度单位 个长度单位 | D.向左平移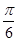 个长度单位 个长度单位 |
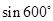 的值为( )
的值为( )
A.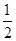 | B.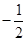 | C.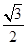 | D.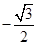 |
已知,函数y=2sin(ωx+θ)为偶函数(0<θ<π) 其图象与直线y=2的交点的横坐标为x1,x2,若| x1-x2|的最小值为π,则 ( )
A.ω=2,θ= | B.ω= ,θ= ,θ= | C.ω= ,θ= ,θ= | D.ω=2,θ= |
[2014·郑州调研]若函数y=2cosωx在区间[0, ]上递减,且有最小值1,则ω的值可以是( )
]上递减,且有最小值1,则ω的值可以是( )
| A.2 | B.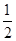 | C.3 | D.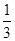 |
 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 ,且当
,且当 时,
时, ,则
,则 的值为
的值为