题目内容
已知,函数y=2sin(ωx+θ)为偶函数(0<θ<π) 其图象与直线y=2的交点的横坐标为x1,x2,若| x1-x2|的最小值为π,则 ( )
A.ω=2,θ= | B.ω= ,θ= ,θ= | C.ω= ,θ= ,θ= | D.ω=2,θ= |
A
解析试题分析:∵函数y=2sin(ωx+θ),且函数y=2sin(ωx+θ)是偶函数,结合所给的选项可得θ=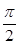 .再由其图象与直线y=2的某两个交点横坐标为x1,x2,|x1-x2|的最小值为π,可得函数的周期为π,即
.再由其图象与直线y=2的某两个交点横坐标为x1,x2,|x1-x2|的最小值为π,可得函数的周期为π,即 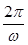 =π,故ω=2,故选A.
=π,故ω=2,故选A.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
函数 的单调递减区间( )
的单调递减区间( )
A. | B. |
C. | D. |
 ( )
( )
A. | B. | C. | D. |
函数
 的值域是( )
的值域是( )
A. | B. | C. | D. |
要得到函数 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向左平行移动 个单位长度 个单位长度 | B.向右平行移动 个单位长度 个单位长度 |
C.向左平行移动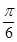 个单位长度 个单位长度 | D.向右平行移动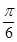 个单位长度 个单位长度 |
设函数f(x)=sin(2x+ ),则下列结论正确的是( )
),则下列结论正确的是( )
A.f(x)的图象关于直线x= 对称 对称 |
B.f(x)的图象关于点( ,0)对称 ,0)对称 |
C.f(x)的最小正周期为π,且在[0, ]上为增函数 ]上为增函数 |
D.把f(x)的图象向右平移 个单位,得到一个偶函数的图象 个单位,得到一个偶函数的图象 |
 的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )
的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )


 的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )



