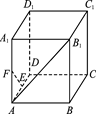
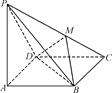
题目内容
正方体 的棱长为1,
的棱长为1, 为
为 的中点,
的中点, 为线段
为线段 的动点,过
的动点,过 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为 ,则下列命题正确的是
,则下列命题正确的是 
①当 时,
时, 为四边形 ②当
为四边形 ②当 时,
时, 为等腰梯形
为等腰梯形
③当 时,
时, 与
与 的交点
的交点 满足
满足 ④当
④当 时,
时, 为六边形
为六边形
⑤当 时,
时, 的面积为
的面积为
①②③⑤
解析试题分析:如图,当 时,,即Q为CC1中点,此时可得
时,,即Q为CC1中点,此时可得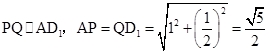 ,
,
故可得截面APQD1为等腰梯形,故②正确;由上图当点Q向C移动时,满足 ,只需在DD1上取点M满足AM∥PQ,即可得截面为四边形APQM,故①正确;③
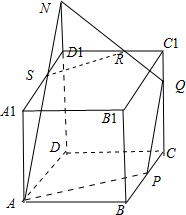
,只需在DD1上取点M满足AM∥PQ,即可得截面为四边形APQM,故①正确;③ 时,如图,
时,如图,
延长DD1至N,使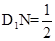 ,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证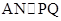 ,由
,由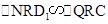 1,可得
1,可得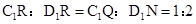 ,故可、
,故可、
得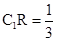 ,故正确;④由③可知当
,故正确;④由③可知当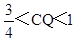 时,只需点Q上移
时,只需点Q上移
即可,此时的截面形状仍然上图所示的APQRS,显然为五边形,故错误;
⑤当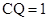 时,Q与C1重合,取A1D1的中点F,连接AF,可证
时,Q与C1重合,取A1D1的中点F,连接AF,可证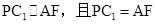 ,可知截面为APC1F为菱形,故其面积为
,可知截面为APC1F为菱形,故其面积为 ,故正确.
,故正确.
考点:空间图形与平面图形的关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
 各棱所在直线中,与棱
各棱所在直线中,与棱 所在直线互为异面直线的有 条.
所在直线互为异面直线的有 条.
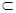 β,则α∥β.
β,则α∥β. 和直线
和直线 ,给出条件:
,给出条件: ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
. ;(2)当满足条件 时,有
;(2)当满足条件 时,有 .
.
 中,
中, 分别是
分别是 的中点.则直线
的中点.则直线 和
和 所成的角为__________.
所成的角为__________.