题目内容
已知函数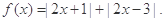
(1)求不等式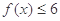 的解集;
的解集;
(2)若关于 的不等式
的不等式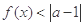 的解集非空,求实数
的解集非空,求实数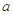 的取值范围.
的取值范围.
(1)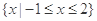 ;(2)
;(2)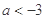 或
或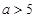
解析试题分析:(1)解决含绝对值的问题往往是要先去绝对值,而绝对值关系为: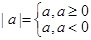 ;本小题需要解不等式,考虑到函数含有两个绝对值,所以分三段去绝对值,建立三个不等式组,然后求出三个不等式,最后取并集;(2)要使
;本小题需要解不等式,考虑到函数含有两个绝对值,所以分三段去绝对值,建立三个不等式组,然后求出三个不等式,最后取并集;(2)要使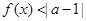 非空,则
非空,则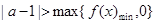 .注意到
.注意到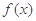 两绝对值对含有
两绝对值对含有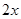 ,利用绝对值性质
,利用绝对值性质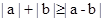 ,
,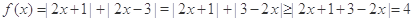 巧妙消去
巧妙消去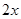 .也可以利用(1)去绝对值得到分段函数然后求函数值域来解.
.也可以利用(1)去绝对值得到分段函数然后求函数值域来解.
试题解析:
原不等式等价于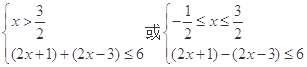 或
或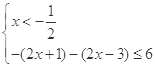 3分
3分
解得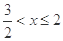 或
或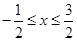 或
或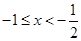 .
.
即不等式的解集为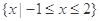 . 5分
. 5分
(2)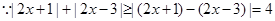 8分
8分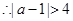
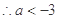 或
或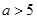 10分.
10分.
考点:(1)含绝对值不等式的解法;(2)由条件求含参不等式参数取值范围.

练习册系列答案
相关题目
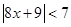 和不等式
和不等式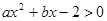 的解集相同,则
的解集相同,则 、
、 的值为
的值为  ,不等式
,不等式 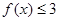 的解集是
的解集是 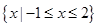
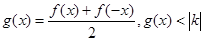 存在实数解,求实数
存在实数解,求实数  的取值范围。
的取值范围。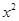 -(
-(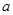 +
+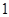 )
)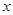 +
+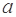 ∈R).
∈R). ,(1)当a=2时,求关于x的不等式
,(1)当a=2时,求关于x的不等式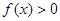 的解集;(2)当a>0时,求关于x的不等式
的解集;(2)当a>0时,求关于x的不等式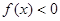 的解集.
的解集.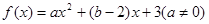 ,
,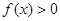 的解集
的解集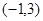 .求
.求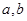 的值;
的值;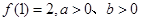 求
求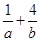 的最小值.
的最小值.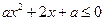 的解集为
的解集为 ,则实数a的取值范围是
,则实数a的取值范围是