Question

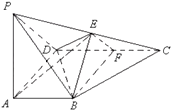
【题目】已知四棱锥，底面是菱形，平面，点为中点，点为中点．

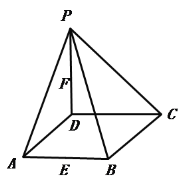
（1） 证明：平面平面；

（2） 求二面角的平面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

(1)先由已知条件证明为等边三角形,可得，利用线面垂直的的性质可证,得到面，进而证明面面；(2)先由二面角的定义找出二面角的平面角，利用余弦定理可求出此角的余弦值.

（1）证明：连BD．∵AB＝AD，∠DAB＝60°，

∴△ADB为等边三角形，∴E是AB中点．∴AB⊥DE，∵PD⊥面ABCD，AB面ABCD，∴AB⊥PD．

∵DE面PED，PD面PED，DE∩PD＝D，

∴AB⊥面PED，∵AB面PAB．∴面PED⊥面PAB．

（2）解：∵AB⊥平面PED，PE面PED，∴AB⊥PE．连结EF，∵ EF面PED，∴AB⊥EF．

∴ ∠PEF为二面角P－AB－F的平面角．

设AD＝2，那么PF＝FD＝1，DE＝．

在△PEF中，PE＝，EF＝2，PF＝1

∴cos∠PEF＝

即二面角P－AB－F的平面角的余弦值为．