题目内容
【题目】将甲、乙两颗骰子先后各抛一次,![]() 分别表示抛掷甲、乙两颗骰子所出现的点数.图中三角形阴影部分的三个顶点为
分别表示抛掷甲、乙两颗骰子所出现的点数.图中三角形阴影部分的三个顶点为![]() 、
、![]() )和
)和![]() .
.
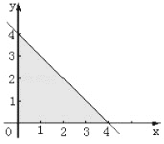
(1)若点![]() 落在如图阴影所表示的平面区域(包括边界)的事件记为
落在如图阴影所表示的平面区域(包括边界)的事件记为![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)若点![]() 落在直线
落在直线![]() (
(![]() 为常数)上,且使此事件的概率
为常数)上,且使此事件的概率![]() 最大,求
最大,求![]() 和
和![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]() ,
,![]() .
.
【解析】
(1)由题意知,本题是一个古典概型,试验发生包含的基本事件总数为6×6,画出图形,满足条件的事件![]() 可以列举出有6个整点,根据古典概型概率公式得到结果.
可以列举出有6个整点,根据古典概型概率公式得到结果.
(2)点![]() 落在
落在![]() (
(![]() 为常数)的直线上,且使此事件的概率最大,只需基本事件最多,由
为常数)的直线上,且使此事件的概率最大,只需基本事件最多,由![]() ,画出图形,直线
,画出图形,直线![]() 过
过![]() 时适合,求得
时适合,求得![]() ,此时有6个整点,得到结果.
,此时有6个整点,得到结果.
基本事件总数为![]() ,
,
如图满足在阴影三角形内的有:
当![]() 时,
时,![]() ,2,3;
,2,3;
当![]() 时,
时,![]() ,2;
,2;
当![]() 时,
时,![]() ﹒
﹒
共有(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)6个点落在条件区域内,
![]() .
.
(2)点![]() 落在
落在![]() (
(![]() 为常数)的直线上,且使此事件的概率最大. 只需基本事件最多.
为常数)的直线上,且使此事件的概率最大. 只需基本事件最多.
由![]() ,将直线
,将直线![]() 平移,如图可知,当
平移,如图可知,当![]() .
.
即当![]() 时,(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)基本事件最多,共有6种
时,(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)基本事件最多,共有6种
此时![]() 最大.
最大.

【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
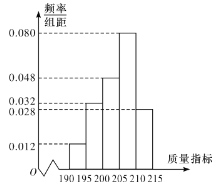
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?
【题目】一商场对每天进店人数和商品销售件数进行了统计对比,得到如下表格:
人数 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件数 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(1)在答题卡给定的坐标系中画出表中数据的散点图,并由散点图判断销售件数![]() 与进店人数
与进店人数![]() 是否线性相关?(给出判断即可,不必说明理由);
是否线性相关?(给出判断即可,不必说明理由);
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
的回归方程(系数精确到0.01),预测进店人数为80时,商品销售的件数(结果保留整数).
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
参考公式: ,
,![]() ,其中
,其中![]() ,
,![]() 为数据
为数据![]() 的平均数.
的平均数.
【题目】大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有250人参与学习先修课程.
(Ⅰ)这两年学校共培养出优等生150人,根据下图等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

优等生 | 非优等生 | 总计 | |
学习大学先修课程 | 250 | ||
没有学习大学先修课程 | |||
总计 | 150 |
(Ⅱ)某班有5名优等生,其中有2名参加了大学生先修课程的学习,在这5名优等生中任选3人进行测试,求这3人中至少有1名参加了大学先修课程学习的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]()
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?


