题目内容
11.已知函数f(x)=2$\sqrt{3}$sinxcosx+2cos2x-1,x∈R.(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)当x∈[-$\frac{π}{12}$,$\frac{π}{2}$]时,实数m满足:m-f(x)≥0恒成立,求实数m的取值范围.
分析 (1)化简可得f(x)=2sin(2x+$\frac{π}{6}$),由周期公式可得;
(2)解不等式2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得函数f(x)的单调递增区间;
(3)由x∈[-$\frac{π}{12}$,$\frac{π}{2}$]和三角函数的值域可得2sin(2x+$\frac{π}{6}$)∈[-1,2],要满足题意只需m大于等于f(x)的最大值2即可.
解答 解:(1)化简可得f(x)=2$\sqrt{3}$sinxcosx+2cos2x-1
=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$可得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
∴函数f(x)的单调递增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z;
(3)当x∈[-$\frac{π}{12}$,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[0,$\frac{7π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],∴2sin(2x+$\frac{π}{6}$)∈[-1,2],
∴实数m满足:m-f(x)≥0恒成立,
∴只需m大于等于f(x)的最大值2
∴实数m的取值范围为[2,+∞).
点评 本题考查三角函数恒等变换,涉及三角函数的单调性和周期性以及值域,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.以下结论不正确的是( )
| A. | 根据2×2列联表中的数据计算得出K2≥6.635,而P(K2≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系 | |
| B. | 在线性回归分析中,相关系数为r,|r|越接近于1,相关程度越大;|r|越小,相关程度越小 | |
| C. | 在回归分析中,相关指数R2越大,说明残差平方和越小,回归效果越好 | |
| D. | 在回归直线y=0.5x-85中,变量x=200时,变量y的值一定是15 |
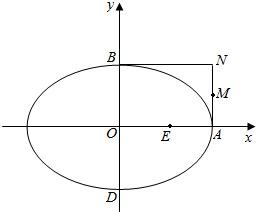 如图所示,椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右顶点是A,上、下两个顶点分别为B、D,四边形OANB是矩形(O为原点),点E、M分别为线段OA、AN的中点.
如图所示,椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右顶点是A,上、下两个顶点分别为B、D,四边形OANB是矩形(O为原点),点E、M分别为线段OA、AN的中点.