题目内容
8.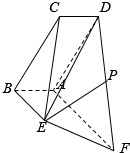 如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF,BC=$\sqrt{2}$AB,∠CBA=$\frac{π}{4}$,P为DF的中点.
如图,已知平行四边形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,AB⊥AF,AB=BE=$\frac{1}{2}$AF,BC=$\sqrt{2}$AB,∠CBA=$\frac{π}{4}$,P为DF的中点.(1)求证:PE∥平面ABCD;
(2)求平面DEF与平面ABCD所成角(锐角)的余弦值.
分析 (I)如图所示,取AD的中点M,连接MP,MB.又P为DF的中点.利用三角形的中位线定理可得$MP\underset{∥}{=}\frac{1}{2}AF$,验证$BE\underset{∥}{=}\frac{1}{2}AF$,可得$MP\underset{∥}{=}BE$,四边形BMPE为平行四边形,得到PE∥BM,可得PE∥平面ABCD;
(II)连接AC,在△ABC中,由余弦定理可得AC=AB,AC⊥AB.由平面ABCD⊥平面ABEF,可得AC⊥平面ABEF.分别以AB,AF,AC为x,y,z轴建立空间直角坐标系,可设AB=1,设平面DEF的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$,可得$\overrightarrow{n}$.取平面ABCD的一个法向量$\overrightarrow{m}$=(0,1,0),利用$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$,即可得出.
解答 (I)证明:如图所示,取AD的中点M,连接MP,MB. 又P为DF的中点.
又P为DF的中点.
∴$MP\underset{∥}{=}\frac{1}{2}AF$,
又∵$BE\underset{∥}{=}\frac{1}{2}AF$,
∴$MP\underset{∥}{=}BE$,
∴四边形BMPE为平行四边形,
∴PE∥BM,
而PE?平面ABCD,BM?平面ABCD,
∴PE∥平面ABCD;
(II)解:连接AC,在△ABC中,BC=$\sqrt{2}$AB,∠CBA=$\frac{π}{4}$,
由余弦定理可得:AC2=BC2+AB2-2BC•ABcos∠CBA=$2A{B}^{2}+A{B}^{2}-2\sqrt{2}A{B}^{2}×\frac{\sqrt{2}}{2}$=AB2,
∴AC=AB,
∴△ABC是等腰直角三角形,AC⊥AB.
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
∴AC⊥平面ABEF.
分别以AB,AF,AC为x,y,z轴建立空间直角坐标系,
设AB=1,则A(0,0,0),B(1,0,0),E(1,1,0),C(0,0,1),D(-1,0,1),F(0,2,0).
∴$\overrightarrow{DE}$=(2,1,-1),$\overrightarrow{DF}$=(1,2,-1).
设平面DEF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{2x+y-z=0}\\{x+2y-z=0}\end{array}\right.$,
令x=1,则y=1,z=3.
∴$\overrightarrow{n}$=(1,1,3).
取平面ABCD的一个法向量$\overrightarrow{m}$=(0,1,0),则$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{11}}$=$\frac{\sqrt{11}}{11}$.
∴平面DEF与平面ABCD所成角(锐角)的余弦值为$\frac{\sqrt{11}}{11}$.
点评 本题考查了线面平行与垂直的判定与性质定理、三角形的中位线定理、平行四边形的判定与性质定理,考查了通过建立空间直角坐标系利用线面垂直的性质定理、向量垂直与数量积的关系及平面的法向量的夹角求出二面角的方法,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案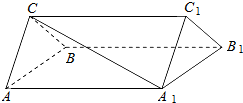 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点 质地均匀的一个转盘,从圆心开始作四个半径,将圆盘分成A,B,C,D四份,它们所对的圆心角依次为45°,60°,120°,135°,端点在圆心的指针可以绕圆心转动,某人进行游戏,规则是随机转动指针,待其自行停下,指针停在A,B,C,D区域可分别得到4,3,2,1分,设指针转动后停在任何一个地方是等可能的,指针停在分界线上时,按高分计算.
质地均匀的一个转盘,从圆心开始作四个半径,将圆盘分成A,B,C,D四份,它们所对的圆心角依次为45°,60°,120°,135°,端点在圆心的指针可以绕圆心转动,某人进行游戏,规则是随机转动指针,待其自行停下,指针停在A,B,C,D区域可分别得到4,3,2,1分,设指针转动后停在任何一个地方是等可能的,指针停在分界线上时,按高分计算. 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.