题目内容
(本小题满分12分)
已知函数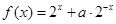 是定义域为
是定义域为 的奇函数,(1)求实数
的奇函数,(1)求实数 的值;(2)证明
的值;(2)证明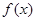 是
是 上的单调函数;(3)若对于任意的
上的单调函数;(3)若对于任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
(1)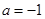
(2)根据定义法,设出变量,作差,变形,定号,下结论,得到证明。
(3)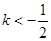
【解析】
试题分析:解:(1)∵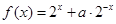 是定义域为
是定义域为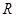 的奇函数,
的奇函数,
∴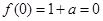 ,∴
,∴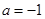 ,
,
经检验当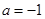 时,
时,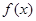 是奇函数,故所求
是奇函数,故所求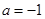 。
。
(2)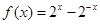 ,
,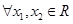 ,且
,且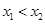 ,
,
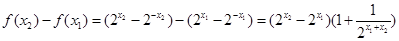
∵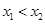 ,∴
,∴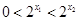 ,即
,即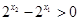 ∴
∴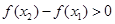 即
即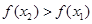 ,
,
∴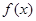 是
是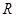 上的递增函数,即
上的递增函数,即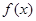 是
是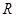 上的单调函数。
上的单调函数。
(3)∵根据题设及(2)知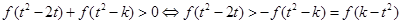
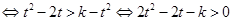 ,
,
∴原不等式恒成立即是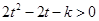 在
在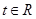 上恒成立,∴
上恒成立,∴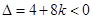 ,…(11分)
,…(11分)
∴所求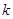 的取值范围是
的取值范围是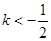 。
。
考点:函数的性质运用
点评:解决该试题的关键是能理解函数的奇偶性以及函数单调性的运用,属于基础题。

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目