题目内容
(本小题满分12分)如图在空间直角坐标系中![]() ,原点
,原点![]() 是
是![]() 的中点,点
的中点,点![]() 的坐标是(
的坐标是(![]() ),点
),点![]() 在平面
在平面![]() 上,且
上,且![]() ,
,![]() .
.
(I)求向量![]() 的坐标;
的坐标;![]()
![]()
![]()
(Ⅱ)设向量![]() 和
和![]() 的夹角为
的夹角为![]() ,求
,求![]() 的值.
的值.

(I){0,-![]() }(Ⅱ)
}(Ⅱ)![]()
解析:
(1)过D作DE⊥BC,垂足为E,在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,得BD=1,CD=![]() ,∴DE=CD·sin30°=
,∴DE=CD·sin30°=![]() .OE=OB-BE=OB-BD·cos60°=1-
.OE=OB-BE=OB-BD·cos60°=1-![]() ,∴D点坐标为(0,-
,∴D点坐标为(0,-![]() ),即向量OD[TX→]的坐标为{0,-
),即向量OD[TX→]的坐标为{0,-![]() }.
}.
(2)依题意:![]() ,
,
所以![]() .
.
设向量![]() 和
和![]() 的夹角为θ,则
的夹角为θ,则
cosθ=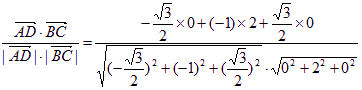
![]() .
.

练习册系列答案
相关题目