题目内容
3.设全集U是实数集R,M={x|y=ln(x2-2x) },N={y|y=$\sqrt{x}+1$},则图中阴影部分表示的集合是( )
| A. | {x|-2≤x<2} | B. | {x|1<x≤2} | C. | {x|1≤x≤2} | D. | {x|x<1} |
分析 由图知,阴影部分表示的集合中的元素是在集合N中的元素但不在集合M中的元素组成的,即N∩CUM.
解答 解:由韦恩图知阴影部分表示的集合为N∩(CUM)
M={x|y=ln(x2-2x) }
∴x2-2x>0,
解得x<0,或x>2,
∴M={x|x<0,或x>2},
∴CUM={x|0≤x≤2}=[0,2],
N={y|y=$\sqrt{x}+1$}={y|y≥1}=[1,+∞),
∴N∩(CUM)=[1,2],
故选:C
点评 本小题主要考查Venn图表达集合的关系及运算、二次不等式的解法等基础知识,属于基础题

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
13.已知点F1、F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点,过F1且垂直于x轴的直线与椭圆交于 M、N两点,若△M NF2为等腰直角三角形,则该椭圆的离心率e为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-1+\sqrt{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
12.设a是第三象限角,cosa=-$\frac{3}{5}$,则tan$\frac{a}{2}$=( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
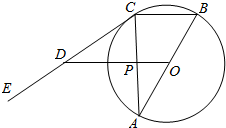 如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O做BC的平行线,分别交EC和AC于点D和点P,求OD.
如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O做BC的平行线,分别交EC和AC于点D和点P,求OD.