题目内容
8.已知数列{an}满足${a_1}=\frac{7}{6}$,${a_{n+1}}=\frac{1}{2}{a_n}+\frac{1}{3}$,(1)当${a_n}≠\frac{2}{3}$时,求证{${a_n}-\frac{2}{3}$}是等比数列;
(2)求数列{an}的通项公式.
分析 (1)通过对${a_{n+1}}=\frac{1}{2}{a_n}+\frac{1}{3}$变形可知an+1-$\frac{2}{3}$=$\frac{1}{2}$(an-$\frac{2}{3}$),利用${a_n}≠\frac{2}{3}$即得结论;
(2)通过(1)及等比数列的求和公式计算即得结论.
解答 (1)证明:∵${a_{n+1}}=\frac{1}{2}{a_n}+\frac{1}{3}$,
∴an+1-$\frac{2}{3}$=$\frac{1}{2}$(an-$\frac{2}{3}$),
又∵${a_n}≠\frac{2}{3}$,
∴an-$\frac{2}{3}$≠0,
∴数列{${a_n}-\frac{2}{3}$}是公比为$\frac{1}{2}$的等比数列;
(2)解:由${a_1}=\frac{7}{6}$及(1)可知,an-$\frac{2}{3}$=($\frac{7}{6}$-$\frac{2}{3}$)•$\frac{1}{{2}^{n-1}}$=$\frac{1}{{2}^{n}}$,
∴an=$\frac{2}{3}$+$\frac{1}{{2}^{n}}$.
点评 本题考查数列的通项,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.若某几何体的三视图如图所示,则此几何体的体积等于( )
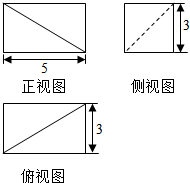

| A. | $\frac{75}{2}$ | B. | 30 | C. | 75 | D. | 15 |
3.设全集U是实数集R,M={x|y=ln(x2-2x) },N={y|y=$\sqrt{x}+1$},则图中阴影部分表示的集合是( )


| A. | {x|-2≤x<2} | B. | {x|1<x≤2} | C. | {x|1≤x≤2} | D. | {x|x<1} |
13.若x1,x2,x3,…,x2013的方差为3,则3x1,3x2,3x3,…,3x2013的方差为( )
| A. | 3 | B. | 9 | C. | 18 | D. | 27 |
20.1升水中有2只微生物,任取0.1升水化验,含有微生物的概率是( )
| A. | 0.01 | B. | 0.19 | C. | 0.1 | D. | 0.2 |