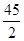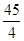题目内容
数列{an}是公比为 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( 为常数,且
为常数,且 ≠1).
≠1).
(I)求数列{an}的通项公式及 的值;
的值;
(Ⅱ)比较 +
+ +
+ + +
+ + 与了
与了 Sn的大小.
Sn的大小.
 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( 为常数,且
为常数,且 ≠1).
≠1).(I)求数列{an}的通项公式及
 的值;
的值;(Ⅱ)比较
 +
+ +
+ + +
+ + 与了
与了 Sn的大小.
Sn的大小.(1)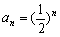
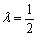 (2)
(2)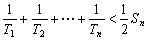
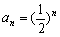
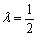 (2)
(2)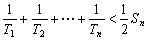
试题分析:解:(Ⅰ)由题意
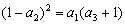 ,即
,即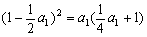
解得
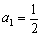 ,∴
,∴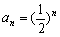 2分
2分又
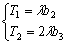 ,即
,即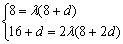 4分
4分解得
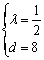 或
或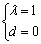 (舍)∴
(舍)∴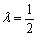 6分
6分(Ⅱ)由(Ⅰ)知
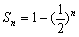 7分
7分∴
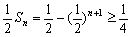 ① 9分
① 9分又
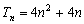 ,
,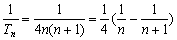 11分
11分∴
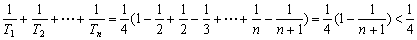 ② 12分
② 12分由①②可知
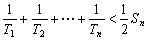 13分
13分点评:解决的关键是根据已知数列的特点,结合裂项法来求和,属于中档题。

练习册系列答案
相关题目
 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第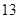 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加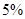 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多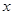 元.
元.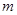 个月还清贷款(
个月还清贷款(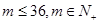 ),试用
),试用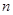 表示小王第
表示小王第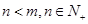 )个月的还款额
)个月的还款额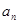 ;
;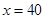 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?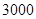 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: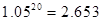 )
) 的前
的前 项和为
项和为 ,
, ,
, ,则数列
,则数列 的前
的前 项和为______________
项和为______________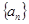 的公差
的公差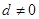 ,且
,且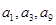 成等比数列,则
成等比数列,则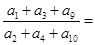 ( )
( )



 中,
中, ,且
,且 成等比数列.
成等比数列. (
( ),求数列
),求数列 的前
的前 项和
项和 .
. 前三项的和为
前三项的和为 ,前三项的积为
,前三项的积为 .
.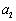 ,
, ,
,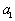 成等比数列,求数列
成等比数列,求数列 的前
的前 项和.
项和.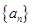 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
 ,求数列
,求数列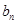 的前
的前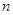 项和
项和
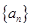 满足
满足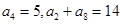 ,数列
,数列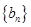 满足
满足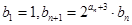 .
.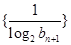 的前
的前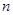 项和;
项和;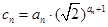 ,求数列
,求数列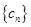 的前
的前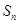 .
.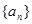 中,已知前
中,已知前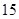 项的和
项的和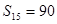 ,则
,则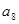 等于
等于