Question

在平面直角坐标系中，我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形．如图，在菱形ABCD中，四个顶点坐标分别是（-8，0），（0，4），（8，0），（0，-4），则菱形ABCD能覆盖的单位格点正方形的个数是     个；若菱形A_nB_nC_n D_n的四个顶点坐标分别为（-2n，0），（0，n），（2n，0），（0，-n）（n为正整数），则菱形A_nB_nC_n D_n能覆盖的单位格点正方形的个数为     （用含有n的式子表示）．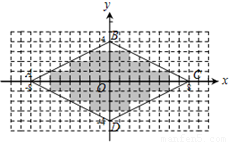

Answer 1

【答案】分析：首先菱形ABCD能覆盖的单位格点正方形的个数可以根据图示直接得到，在一个象限的格点正方形的个数都是4×3，然后乘以4即可求出菱形ABCD能覆盖的单位格点正方形的个数；利用这个规律可以得到菱形A_nB_nC_nD_n的能覆盖的单位格点正方形的个数．
解答：解：∵菱形ABCD的四个顶点坐标分别是（-8，0），（0，4），（8，0），（0，-4），
∴菱形ABCD能覆盖的单位格点正方形的个数是4×4×3=48个；
∵菱形A_nB_nC_nD_n的四个顶点坐标分别为（-2n，0），（0，n），（2n，0），（0，-n）（n为正整数），
∴菱形A_nB_nC_nD_n能覆盖的单位格点正方形的个数为4×n×（n-1）=4n²-4n．
故答案为：48；4n²-4n．
点评：此题主要考查简单的合情推理，考查菱形的性质、正方形的性质、直角坐标系的点的坐标特点等知识点，首先根据具体的图形找规律，然后利用规律得到一般结论．