题目内容

直线x=0，y=0，x=2与y=(
2
)2所围成的图形绕X轴旋转一周而成的旋转体的体积等于
 
．
分析：本题考查的知识点是组合几何体的面积、体积问题，由已知得直线x=0，y=0，x=2与曲线y=(
2
)2所围成的图形为一个边长为2的正方形，绕X轴旋转一周而成的旋转体为一个底面半径为2，高为2的圆柱，代入圆柱体积公式，易得答案．
解答：解：∵直线x=0，y=0，x=2与y=(
2
)2所围成的图形边长为2的正方形，
其绕X轴旋转一周而成的旋转体为一个底面半径为2，高为2的圆柱
则V=πr2h=π×22×2=8π
故答案为：8π
点评：要求一个圆柱体的体积，关键是要结合已知条件，分析出圆柱的底面半径和高，然后代入圆柱体积公式即可得到答案．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
将一枚骰子随机地向上抛掷两次，记朝上的点数分别为x，y．
（1）求点（x，y）恰好在直线2x+y-7=0上的概率；
（2）求点（x，y）恰好落在由三条直线x=0，y=0，2x+y-7=0围成的三角形内部（不包括边界）的概率：
设点P（x0，y0）在直线x=m（y≠±m，0＜m＜1）上，过点P作双曲线x2-y2=1的两条切线PA、PB，切点为A、B，定点M（，0），
（1）求证：三点A、M、B共线；
（2）过点A作直线x-y=0的垂线，垂足为N，试求△AMN的重心G所在曲线方程。
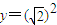直线x=0，y=0，x=2与所围成的图形绕X轴旋转一周而成的旋转体的体积等于    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网