Question

下列几个命题：
①方程x²+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；
②函数y=

x2-1

+

1-x2

是偶函数，但不是奇函数；
③曲线y=|3-x²|和直线y=a（a∈R）的公共点个数是m，则m的值不可能是1．
其中正确的有

 

．（填序号）

Answer 1

分析：①根据一元二次方程有异号根的判定方法可知①正确；②求出函数的定义域，根据定义域确定函数的解析式y=0，故②错；③画出函数的图象，根据图象可知③正确．

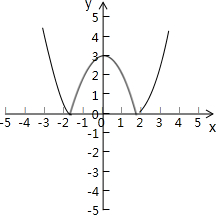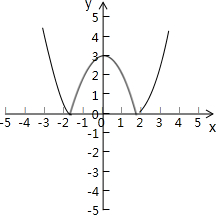解答：解：①方程x²+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；正确；
②函数的定义域为{-1，1}，∴y=0既是奇函数又是偶函数，故②错；
③根据函数y=|3-x²|的图象可知，正确．
故答案为①③．

点评：此题是个基础题．考查函数图象的对称变化和一元二次方程根的问题，以及函数奇偶性的判定方法等基础知识，考查学生灵活应用知识分析解决问题的能力．