题目内容
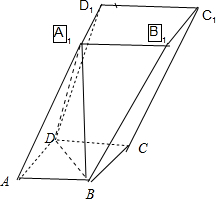
(2010•昆明模拟)在平行六面体ABCD-A1B1C1D1中,点A1在底面ABCD内的射影恰好为点B,若AB=AD=
AA1,∠BAD=60°,则异面直线A1B与B1C所成角为( )
| 1 |
| 2 |
分析:先根据A1D∥B1C得到∠DA1B(或其补角)即为异面直线A1B与B1C所成角;然后通过点A1在底面ABCD内的射影恰好为点B的对应结论:A1B⊥平面ABCD求出RT△A1BD中两直角边长,进而求出角的度数.
解答:解:∵在平行六面体ABCD-A1B1C1D1中,A1D∥B1C,
∴∠DA1B(或其补角)即为异面直线A1B与B1C所成角
设AB=AD=a,则AA1=2a,
∵点A1在底面ABCD内的射影恰好为点B
∴A1B⊥平面ABCD,A1B=
=
a;
∵∠BAD=60°,AB=AD,
∴BD=a,
在RT△A1BD中,tan∠DA1B=
=
=
,
∴∠DA1B=30°.
即异面直线A1B与B1C所成角:30°.
故选:A.
∴∠DA1B(或其补角)即为异面直线A1B与B1C所成角

设AB=AD=a,则AA1=2a,
∵点A1在底面ABCD内的射影恰好为点B
∴A1B⊥平面ABCD,A1B=
| AA 12-AB 2 |
| 3 |
∵∠BAD=60°,AB=AD,
∴BD=a,
在RT△A1BD中,tan∠DA1B=
| BD |
| A1B |
| a | ||
|
| ||
| 3 |
∴∠DA1B=30°.
即异面直线A1B与B1C所成角:30°.
故选:A.
点评:本题主要考查异面直线及其所成的角.求异面直线所成角的关键在于通过作平行线,把异面直线所成角的问题转化为相交直线所成的角.

练习册系列答案
相关题目
 (2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )
(2010•昆明模拟)如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有( )