题目内容
(本小题满分12分)
已知数列
满足
，且对任意
，都有
．
(Ⅰ）求证：数列
为等差数列,并求的通项公式；
(Ⅱ）试问数列中
是否仍是中的项？如果是，请指出是数列的第几项；如果不是，请说明理由．
解: （Ⅰ）
，即
，
所以
，
所以数列
是以
为首项，公差为
的等差数列． ……4分
可得数列的通项公式为
，所以
．…………………… 6分
（II）
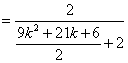
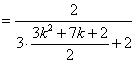． …… 8分
因为
， …… 10分
当
时，
一定是正整数，所以
是正整数．
(也可以从k的奇偶性来分析)
所以
是数列
中的项，是第项． …… 12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
