题目内容
定理:已知O,A,B三点不共线,若点P在直线AB上,且
=λ
λ2
则λ1+λ2=1,类比该定理进行研究,可以得出:已知O、A、B三点不共线,若点P、O在直线AB同侧(点P不在直线AB上),且
=λ1
λ2
,则______.
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
延长OP至Q,令OQ在直线AB上,
则存在实数a使得
=a
,
∵P、O在直线AB同侧
∴|
|<|
|
∴a<1
又∵则存在实数μ1,μ2,使
=μ1
+μ2
且μ1+μ2=1
∴
=λ1
+λ2
=aμ1
+aμ2
即λ1+λ2=a(μ1+μ2)<1
故答案为:λ1+λ2<1
则存在实数a使得
| OP |
| OQ |
∵P、O在直线AB同侧
∴|
| OP |
| OQ |
∴a<1
又∵则存在实数μ1,μ2,使
| OQ |
| OA |
| OB |
∴
| OP |
| OA |
| OB |
| OA |
| OB |
即λ1+λ2=a(μ1+μ2)<1
故答案为:λ1+λ2<1

练习册系列答案
相关题目
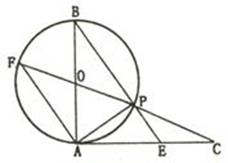
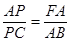
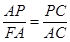
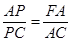 ∵AB=AC
∴
∵AB=AC
∴ ,且
,且 =1,
=1,
 .
. (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与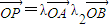 则λ1+λ2=1,类比该定理进行研究,可以得出:已知O、A、B三点不共线,若点P、O在直线AB同侧(点P不在直线AB上),且
则λ1+λ2=1,类比该定理进行研究,可以得出:已知O、A、B三点不共线,若点P、O在直线AB同侧(点P不在直线AB上),且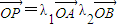 ,则 .
,则 .