题目内容
已知双曲线C1的渐近线方程是y=±
x,且它的一条准线与渐近线y=
x及x轴围成的三角形的周长是
(1+
).以C1的两个顶点为焦点,以C1的焦点为顶点的椭圆记为C2.
(1)求C2的方程;
(2)已知斜率为
的直线l经过定点P(m,0)(m>0)并与椭圆C2交于不同的两点A、B,若对于椭圆C2上任意一点M,都存在θ∈[0,2π],使得
=cosθ•
+sinθ•
成立.求实数m的值.
| ||
| 3 |
| ||
| 3 |
| 3 |
| 2 |
| 3 |
(1)求C2的方程;
(2)已知斜率为
| 1 |
| 2 |
| OM |
| OA |
| OB |
(1)由题意知双曲线C1的焦点在x轴上,设C1的方程为:
-
=1(a>0,b>0)
+
•
=
(1+
)
解得之:
,
∴双曲线的半焦距c=2,椭圆C2方程为:
+y2=1…(4分)
(2)设点M(x,y)及点A(x1,y1),B(x2,y2),
直线AB的方程为:x-2y-m=0,
联立方程组
消去x得8y2+4my+m2-4=0…(6分)
判断式△=16m2-32(m2-4)=16(8-m2)>0
又m>0∴0<m<2
y1y2=
x1x2=(2y1+m)(2y2+m)
=4y1y2+2m(y1+y2)+m2
=
+2m(-
)+m2=
…(7分)
由
=cosθ•
+sinθ•
,可得
…(8分)
代入椭圆方程得4=x2+4y2=(x1cosθ+x2sinθ)2+4(y1cosθ+y2sinθ)2
=(x12+4y12)cos2θ+(x22+4y22)sin2θ+2sinθcosθ(x1x2+4y1y2)
=4(cos2θ+sin2θ)+sin2θ•(x1x2+4y1y2)
即得:sin2θ•(x1x2+4y1y2)=0…(10分)
又∵θ∈[0,2π]的任意性,知:
x1x2+4y1y2=
+4×
=m2-4=0
∵m∈(0,2
)
∴m=2,即满足条件的实数m的值为2 …(12分)
| x2 |
| a2 |
| y2 |
| b2 |
|
1+(
|
| a2 | ||
|
| 3 |
| 2 |
| ||
| 3 |
解得之:
|
∴双曲线的半焦距c=2,椭圆C2方程为:
| x2 |
| 4 |
(2)设点M(x,y)及点A(x1,y1),B(x2,y2),
直线AB的方程为:x-2y-m=0,
联立方程组
|
判断式△=16m2-32(m2-4)=16(8-m2)>0
又m>0∴0<m<2
| 2 |
y1y2=
| (m2-4) |
| 8 |
=4y1y2+2m(y1+y2)+m2
=
| (m2-4) |
| 2 |
| m |
| 2 |
| (m2-4) |
| 2 |
由
| OM |
| OA |
| OB |
|
代入椭圆方程得4=x2+4y2=(x1cosθ+x2sinθ)2+4(y1cosθ+y2sinθ)2
=(x12+4y12)cos2θ+(x22+4y22)sin2θ+2sinθcosθ(x1x2+4y1y2)
=4(cos2θ+sin2θ)+sin2θ•(x1x2+4y1y2)
即得:sin2θ•(x1x2+4y1y2)=0…(10分)
又∵θ∈[0,2π]的任意性,知:
x1x2+4y1y2=
| m2-4 |
| 2 |
| m2-4 |
| 8 |
∵m∈(0,2
| 2 |
∴m=2,即满足条件的实数m的值为2 …(12分)

练习册系列答案
相关题目
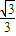 x,且它的一条准线与渐近线y=
x,且它的一条准线与渐近线y=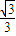 x及x轴围成的三角形的周长是
x及x轴围成的三角形的周长是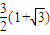 .以C1的两个顶点为焦点,以C1的焦点为顶点的椭圆记为C2.
.以C1的两个顶点为焦点,以C1的焦点为顶点的椭圆记为C2. 的直线l经过定点P(m,0)(m>0)并与椭圆C2交于不同的两点A、B,若对于椭圆C2上任意一点M,都存在θ∈[0,2π],使得
的直线l经过定点P(m,0)(m>0)并与椭圆C2交于不同的两点A、B,若对于椭圆C2上任意一点M,都存在θ∈[0,2π],使得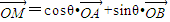 成立.求实数m的值.
成立.求实数m的值.