题目内容
已知双曲线C1的渐近线为y=±
解:设双曲线C1的方程为x2-![]() =λ,将点(
=λ,将点(![]() ,
,![]() )代入得λ=
)代入得λ=![]() ,
,
C1:4x2-![]() y2=1,其焦点坐标为(±1,0).
y2=1,其焦点坐标为(±1,0).
设椭圆C2的方程为![]() +
+![]() =1,其中b>0,将l的方程代入并整理得(2b2+1)x2+6(b2+1)x+(9-b2)(b2+1)=0.
=1,其中b>0,将l的方程代入并整理得(2b2+1)x2+6(b2+1)x+(9-b2)(b2+1)=0.
∵l与C2有公共点,∴Δ≥0,解得b2≥4,b≥2,2b≥4,即短轴长最短为4.
当b=2时,上述方程为9x2+30x+25=0,这时x=-![]() ,y=x+3=
,y=x+3=![]() ,
,
即当l与C2的公共点为(-![]() ,
,![]() )时,C2的短轴长最短为4,椭圆的方程
)时,C2的短轴长最短为4,椭圆的方程![]() +
+![]() =1.
=1.

练习册系列答案
相关题目
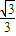 x,且它的一条准线与渐近线y=
x,且它的一条准线与渐近线y=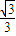 x及x轴围成的三角形的周长是
x及x轴围成的三角形的周长是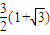 .以C1的两个顶点为焦点,以C1的焦点为顶点的椭圆记为C2.
.以C1的两个顶点为焦点,以C1的焦点为顶点的椭圆记为C2. 的直线l经过定点P(m,0)(m>0)并与椭圆C2交于不同的两点A、B,若对于椭圆C2上任意一点M,都存在θ∈[0,2π],使得
的直线l经过定点P(m,0)(m>0)并与椭圆C2交于不同的两点A、B,若对于椭圆C2上任意一点M,都存在θ∈[0,2π],使得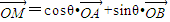 成立.求实数m的值.
成立.求实数m的值.