题目内容
给出下列命题:
①在△ABC中,若
•
>0,∠A为锐角.
②函数y=x3在R上既是奇函数又是增函数.
③不等式x2-4ax+3a2<0的解集为{x|a<x<3a}.
④函数y=f(x)的图象与直线x=a至多有一个交点.
其中正确命题的序号是
①在△ABC中,若
| AB |
| CA |
②函数y=x3在R上既是奇函数又是增函数.
③不等式x2-4ax+3a2<0的解集为{x|a<x<3a}.
④函数y=f(x)的图象与直线x=a至多有一个交点.
其中正确命题的序号是
②④
②④
.(把你认为正确命题的序号都填上)分析:根据向量夹角的定义及数量积的定义,可判断①; 判断函数当的奇偶性及单调性,可判断②;分类讨论不等式解集的情况,可判断③;根据函数的定义,可判断④
解答:解:在△ABC中,若
•
>0,则向量
,
的夹角为锐角,由于两个向量首尾相接,故它们的夹角与A互补,故A为钝角,故①错误;
令f(x)=x3,f(-x)=-f(x),即函数为奇函数,又由f′(x)=3x2≥0恒成立,故函数为增函数,故②正确
当a<0时,不等式x2-4ax+3a2<0的解集为{x|3a<x<a}
当a=0时,不等式x2-4ax+3a2<0的解集为∅;
当a>0时,不等式x2-4ax+3a2<0的解集为{x|a<x<3a},故③错误;
设函数y=f(x)的定义域为A,当a∈A时,函数y=f(x)的图象与直线x=a有一个交点,
当a∉A时,函数y=f(x)的图象与直线x=a无交点,故④正确
故正确的命题序号为:②④
故答案为:②④
| AB |
| CA |
| AB |
| CA |
令f(x)=x3,f(-x)=-f(x),即函数为奇函数,又由f′(x)=3x2≥0恒成立,故函数为增函数,故②正确
当a<0时,不等式x2-4ax+3a2<0的解集为{x|3a<x<a}
当a=0时,不等式x2-4ax+3a2<0的解集为∅;
当a>0时,不等式x2-4ax+3a2<0的解集为{x|a<x<3a},故③错误;
设函数y=f(x)的定义域为A,当a∈A时,函数y=f(x)的图象与直线x=a有一个交点,
当a∉A时,函数y=f(x)的图象与直线x=a无交点,故④正确
故正确的命题序号为:②④
故答案为:②④
点评:本题以命题的真假判断为载体考查了向量的夹角,函数的奇偶性与单调性,解不等式,函数的定义等知识点,难度不大,属于基础题.

练习册系列答案
相关题目
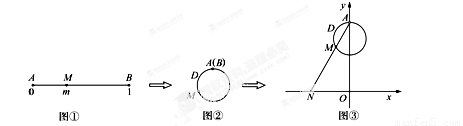
 到实数集R的映射过程:区间
到实数集R的映射过程:区间 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为 ,则m的象就是n,记作
,则m的象就是n,记作 .
.
 ;
; 在定义域
在定义域 上单调递增;
上单调递增; ;
; 的不等式
的不等式 的解集为
的解集为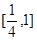 .
.
 ”的否命题为“若
”的否命题为“若 ”
” ”的否定是“
”的否定是“ ”
”