题目内容
(本题满分8分)
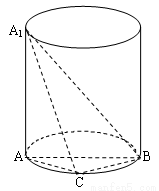
如图,A1A是圆柱的母线,AB是圆柱底面圆的直径, C是底面圆周上异于A,B的任意一点,A1A= AB=2.
(Ⅰ)求证: BC⊥平面A1AC;
(Ⅱ)求三棱锥A1-ABC的体积的最大值.
【答案】
(Ⅰ)略
(Ⅱ)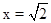 时,三棱锥A1-ABC的体积的最大值为
时,三棱锥A1-ABC的体积的最大值为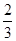 .
.
【解析】证明:∵C是底面圆周上异于A,B的任意一点,且AB是圆柱底面圆的直径,
∴BC⊥AC, ∵AA1⊥平面ABC,BCÌ平面ABC,∴AA1⊥BC,
∵AA1∩AC=A,AA1Ì平面AA1 C,ACÌ平面AA1 C,
∴BC⊥平面AA1C. (3分)
(2)设AC=x,在Rt△ABC中, 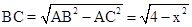 (0<x<2) ,
(0<x<2) ,
故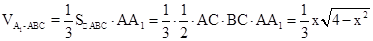 (0<x<2), (5分)
(0<x<2), (5分)
即 .
.
∵0<x<2,0<x2<4,∴当x2=2,
即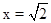 时,三棱锥A1-ABC的体积的最大值为
时,三棱锥A1-ABC的体积的最大值为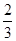 . (8分)
. (8分)

练习册系列答案
相关题目
 中,
中,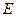 是
是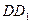 的中点,
的中点,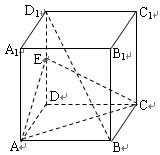
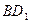 ∥平面
∥平面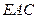 ;
;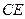 所成角的余弦值.
所成角的余弦值.
 中,
中,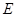 、
、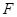 、
、 分别是
分别是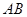 、
、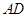 、
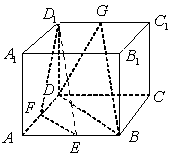
、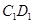 的中点.求证:平面
的中点.求证:平面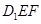 ∥平面
∥平面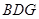 .
.
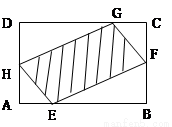
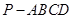 中,底面为直角梯形,
中,底面为直角梯形,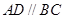 ,
,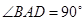 ,
,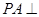 底面
底面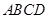 ,且
,且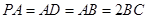 ,
,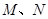 分别为
分别为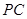 、
、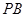 的中点。
的中点。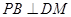 ;
;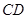 与平面
与平面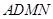 所成角的正弦值。
所成角的正弦值。