题目内容
已知函数 的图象上移动时,点
的图象上移动时,点 的图象上移动.
的图象上移动.(I)点P的坐标为(1,-1),点Q也在y=f(x)的图象上,求t的值;
(Ⅱ)求函数y=g(x)的解析式;
(Ⅲ)若方程
 的解集是∅,求实数t的取值范围.
的解集是∅,求实数t的取值范围.
【答案】分析:(I)由已知中点P的坐标为(1,-1),我们可以求出点Q的坐标(含参数t),由点Q也在y=f(x)的图象上,可以构造一个关于t的方程,解方程求出t的值.
(II)由已知中点 的图象上,可得
的图象上,可得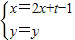 ,由点P(x,y)在y=f(x)的图象上,满足y=f(x)的解析式,代入即可求得函数y=g(x)的解析式;
,由点P(x,y)在y=f(x)的图象上,满足y=f(x)的解析式,代入即可求得函数y=g(x)的解析式;
(III)若方程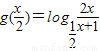 的解集是∅,则方程组
的解集是∅,则方程组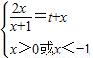 无解,构造函数h(x)=
无解,构造函数h(x)=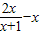 ,求出函数的值域后,即可得到方程
,求出函数的值域后,即可得到方程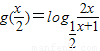 的解集是∅时,实数t的取值范围.
的解集是∅时,实数t的取值范围.
解答:解:(I)当点P坐标为(1,-1),点Q的坐标为(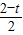 ,-1),
,-1),
∵点Q也在y=f(x)的图象上,∴-1=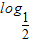 (
(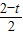 +1)
+1)
∴t=0.
(Ⅱ)设Q(x,y)在y=g(x)的图象上,
则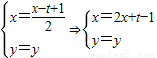
而点P(x,y)在y=f(x)的图象上.
∴y=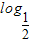 (2x+t)即为所求
(2x+t)即为所求
(Ⅲ)原方程可化为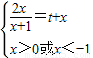
令h(x)=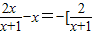 +(x+1)]+3
+(x+1)]+3
①当x>0时,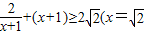 -1时取等号)∴h(x)≤3-2
-1时取等号)∴h(x)≤3-2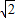 ;
;
②当x<-1时,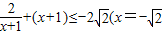 -1时取等号),∴h(x)≥3+2
-1时取等号),∴h(x)≥3+2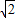
故方程h(x)=t的解集为ϕ时,t的取值范围为(3-2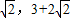 ).
).
点评:本题考查的知识点是对数函数的图象与性质的综合应用,求对数函数的解析式,其中利用坐标系,求出函数y=g(x)的解析式中解答本题的关键.
(II)由已知中点
 的图象上,可得
的图象上,可得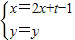 ,由点P(x,y)在y=f(x)的图象上,满足y=f(x)的解析式,代入即可求得函数y=g(x)的解析式;
,由点P(x,y)在y=f(x)的图象上,满足y=f(x)的解析式,代入即可求得函数y=g(x)的解析式;(III)若方程
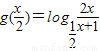 的解集是∅,则方程组
的解集是∅,则方程组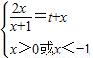 无解,构造函数h(x)=
无解,构造函数h(x)=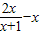 ,求出函数的值域后,即可得到方程
,求出函数的值域后,即可得到方程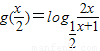 的解集是∅时,实数t的取值范围.
的解集是∅时,实数t的取值范围.解答:解:(I)当点P坐标为(1,-1),点Q的坐标为(
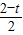 ,-1),
,-1),∵点Q也在y=f(x)的图象上,∴-1=
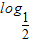 (
(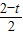 +1)
+1)∴t=0.
(Ⅱ)设Q(x,y)在y=g(x)的图象上,
则
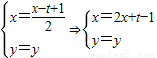
而点P(x,y)在y=f(x)的图象上.
∴y=
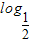 (2x+t)即为所求
(2x+t)即为所求(Ⅲ)原方程可化为
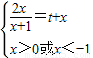
令h(x)=
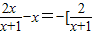 +(x+1)]+3
+(x+1)]+3①当x>0时,
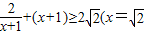 -1时取等号)∴h(x)≤3-2
-1时取等号)∴h(x)≤3-2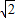 ;
;②当x<-1时,
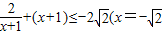 -1时取等号),∴h(x)≥3+2
-1时取等号),∴h(x)≥3+2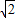
故方程h(x)=t的解集为ϕ时,t的取值范围为(3-2
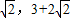 ).
).点评:本题考查的知识点是对数函数的图象与性质的综合应用,求对数函数的解析式,其中利用坐标系,求出函数y=g(x)的解析式中解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
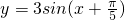 的图象为C,为了得到函数
的图象为C,为了得到函数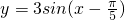 的图象,只需把C上所有的点
的图象,只需把C上所有的点 个单位
个单位 个单位
个单位