题目内容
3.若点P是函数f(x)=x2-lnx上任意一点,则点P到直线x-y-2=0的最小距离为$\sqrt{2}$.分析 设x-y+m=0与函数f(x)=x2-lnx的图象相切于点P(x0,y0).f′(x)=2x-$\frac{1}{x}$,则$2{x}_{0}-\frac{1}{{x}_{0}}$=1,x0>0,解得x0.再利用点到直线的距离公式即可得出.
解答 解:设x-y+m=0与函数f(x)=x2-lnx的图象相切于点P(x0,y0).
f′(x)=2x-$\frac{1}{x}$,则$2{x}_{0}-\frac{1}{{x}_{0}}$=1,x0>0,解得x0=1.
∴y0=1,
∴点P(1,1)到直线x-y-2=0的距离为最小距离d=$\frac{|1-1-2|}{\sqrt{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了利用导数研究切线的斜率、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.若集合{a,b,c}当中的元素是△ABC的三边长,则该三角形是( )
| A. | 正三角形 | B. | 等腰三角形 | C. | 不等边三角形 | D. | 等腰直角三角形 |
11.执行如图所示的程序框图,则输出的S=( )
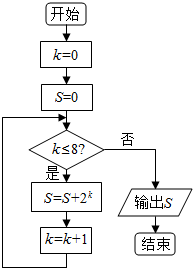

| A. | 1023 | B. | 512 | C. | 511 | D. | 255 |
8.已知m,n是不同的直线,α,β是不同的平面,则下列结论正确的是( )
| A. | 若m∥α,n∥α则m∥n | B. | 若m?α,m∥n,则n∥α | C. | 若m⊥α,α⊥β,则m∥β | D. | 若m⊥α,n∥α,则m⊥n |
15.设f(x)=$\left\{\begin{array}{l}{x-2,(x≥10)}\\{{x}^{2}-1,(x<10)}\end{array}\right.$,则f(5)的值为( )
| A. | 3 | B. | 8 | C. | 24 | D. | 25 |
13.已知函数f(x),当x∈(0,1]时满足如下性质:f(x)=2lnx且$f(x)=2f(\frac{1}{x})$,若在区间$[\frac{1}{3},3]$内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{4ln3}{3},\frac{4}{e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{4}{e})$ |