题目内容
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.
(注:本小题结果可用分数表示)
(Ⅰ)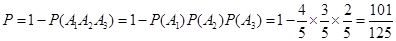 .
.
(Ⅱ)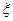 的分布列为
的分布列为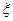
1 2 3 
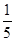
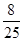
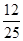
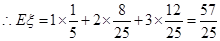
解析试题分析:(Ⅰ)记“该选手能正确回答第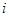 轮的问题”的事件为
轮的问题”的事件为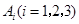 ,
,
则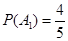 ,
,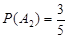 ,
,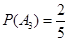 .
. 该选手被淘汰的概率
该选手被淘汰的概率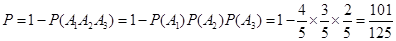 .
.
(Ⅱ)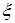 的可能值为1,2,3
的可能值为1,2,3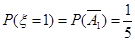 ;
;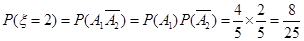 ;
;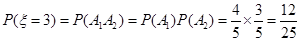 .
. 的分布列为
的分布列为
1 2 3 
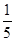
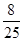
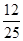
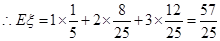
考点:独立事件的概率计算,随机变量的分布列及其数学期望。
点评:典型题,涉及概率计算,随机变量的分布列及其数学期望等问题,是高考经常考查的题型,此类问题,关键是明确基本事件,正确运用概率计算公式,细心计算。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2013年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5浓度 (微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 5 | 0.25 |
| 第二组 | (25,50] | 10 | 0.5 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100) | 2 | 0.1 |
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
 、
、 两名教师被同时分配到甲学校的概率;
两名教师被同时分配到甲学校的概率; 为这四名教师中分配到甲学校的人数,求
为这四名教师中分配到甲学校的人数,求 , B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是
, B小区已经收到邀请的人选择参加“幸福愿景”座谈会的概率是 .
. ,试求
,试求 ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是 .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求 人参加当天的闯关比赛,已知甲获奖的概率为
人参加当天的闯关比赛,已知甲获奖的概率为 ,乙获奖的概率为
,乙获奖的概率为 ,丙获奖而甲没有获奖的概率为
,丙获奖而甲没有获奖的概率为 。
。 ,
,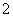 ,
,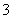 的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为
的三个小球,现从这个盒子中,有放回地先后抽得两个小球的标号分别为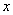 、
、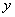 ,设
,设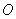 为坐标原点,设
为坐标原点,设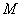 的坐标为
的坐标为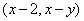 .
. 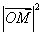 的所有取值之和;
的所有取值之和;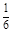 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料.