题目内容
若实数a,b满足a≥0,b≥0,且ab=0,则称a与b互补.记φ(a,b)= -a-b,那么φ(a,b)=0是a与b互补的( )
-a-b,那么φ(a,b)=0是a与b互补的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
C
解析

练习册系列答案
相关题目
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个命题:
有如下四个命题:
① ; ②函数
; ②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,使得
,使得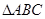 为等边三角形.
为等边三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
下列命题为特称命题的是( )
| A.偶函数的图像关于y轴对称 | B.正四棱柱都是平行六面体 |
| C.不相交的两条直线是平行直线 | D.存在实数大于等于3 |
给定两个命题 ,
, .若
.若 是
是 的必要而不充分条件,则
的必要而不充分条件,则 是
是 的( )
的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p:
 ,命题q:
,命题q:
 ,则下列命题中为真命题的是()
,则下列命题中为真命题的是()
| A.p∧q | B. p∧q p∧q | C.p∧ q q | D. p∧ p∧ q q |
以下有关命题的说法错误的是( )
| A.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| B.“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C.若p∧q为假命题,则p、q均为假命题 |
| D.对于命题p:?x∈R,使得x2+x+1<0,则綈p:?x∈R,有x2+x+1≥0 |
若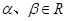 ,且
,且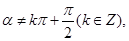
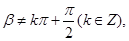 则“
则“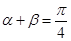 ”是“
”是“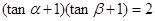 ”的( )
”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要 |
给出命题:已知实数a、b满足a+b=1,则ab≤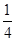 .它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
.它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
| A.0 |
| B.1 |
| C.2 |
| D.3 |
已知命题p: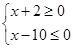 命题q:1-m≤x≤1+m,m>0,若¬p是¬q的必要不充分
命题q:1-m≤x≤1+m,m>0,若¬p是¬q的必要不充分
条件,则实数m的取值范围是( )
| A.m≥0 |
| B.m≥9 |
| C.m≤9 |
| D.m≤-2 |