题目内容
(本小题满分12分)
已知函数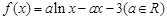 .
.
(I)当 时,求函数
时,求函数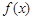 的单调区间;
的单调区间;
(II)若函数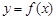 的图象在点
的图象在点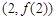 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
【答案】
(1)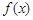 在(0,1)上单调递增,在(1,+∞)上单调递减.
在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)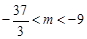 。
。
【解析】
试题分析:
(I)当 时,
时,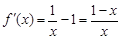 ,
,
令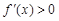 时,解得
时,解得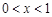 ,所以
,所以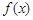 在(0,1)上单调递增;
在(0,1)上单调递增;
令 时,解得
时,解得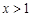 ,所以
,所以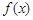 在(1,+∞)上单调递减.
在(1,+∞)上单调递减.
(II)因为函数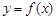 的图象在点(2,
的图象在点(2,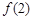 )处的切线的倾斜角为45o,
)处的切线的倾斜角为45o,
所以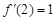 .
.
所以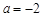 ,
,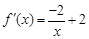 .
.

 ,
,
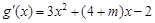 ,
,
因为任意的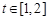 ,函数
,函数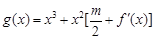 在区间
在区间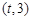 上总存在极值,
上总存在极值,
所以只需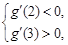
解得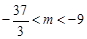 .
.
考点:利用导数研究函数的单调性和极值;导数的几何意义。
点评:(1)本题注意考查导数知识的运用,利用导数来研究函数的单调性很热极值,同时也考查了学生分析问题、解决问题的能力,属于中档题.(2)利用导数求函数的单调区间,一定要先求函数的定义域。(3)要满足函数y=f(x)在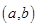 内有极值点。只需满足
内有极值点。只需满足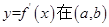 内有变号零点。
内有变号零点。

练习册系列答案
相关题目