题目内容
记函数f(x)的定义域为D,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为坐标的点为函数f(x)图象上的不动点.
为坐标的点为函数f(x)图象上的不动点.
(1)若函数![]() 图象上有两个关于原点对称的不动点,求a,b应满足的条件;
图象上有两个关于原点对称的不动点,求a,b应满足的条件;
(2)在(1)的条件下,若a=8,记函数f(x) 图象上有两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标![]() >3,求点P到直线A1A2距离的最小值及取得最小值时的坐标;
>3,求点P到直线A1A2距离的最小值及取得最小值时的坐标;
(3)下述命题:“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,给予证明;若不正确,请举一反例.
解:(1)若![]() 为函数f(x)不动点,则有
为函数f(x)不动点,则有![]() ,
,
整理得 ![]() ①
①
根据题意可判断方程①有两个根,且这两个根互为相反数,得
![]() >4a 且
>4a 且![]() ,
,![]() <0
<0
所以b=3 ,a>0
而![]() ,所以
,所以![]() .
.
即b=3,a>0,且a≠9.
(2)在(1)的条件下,当a=8时,![]() .
.
由![]() ,解得两个不动点为
,解得两个不动点为![]() ,
,
设点P(x ,y),则y>3 ,即![]() >3解得x<-3 .
>3解得x<-3 .
设点P(x,y)到直线A1A2的距离为d,则
![]()
![]() .
.
当且仅当![]() ,即x=―4时,取等号,此时P(―4,4).
,即x=―4时,取等号,此时P(―4,4).
(3)命题正确.
因为f(x)定义在R上的奇函数,所以f(―0)=―f(0) ,所以0是奇函数f(x)的一个不动点.
设c≠0是奇函数f(x)的一个不动点,则f(c)=c ,由![]() ,所以―c也是f (x)的一个不动点.
,所以―c也是f (x)的一个不动点.
所以奇函数f(x)的非零不动点如果存在,则必成对出现,故奇函数f(x)的不动点数目是奇数个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
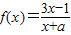 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;