题目内容
记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以(x0,x0)为坐标的点为函数f(x)图象上的不动点.
(1)若函数f(x)=
图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
(2)设点P(x,y)到直线y=x的距离d=
.在(1)的条件下,若a=8,记函数f(x)图象上的两个不动点分别为A1,A2,P为函数f(x)图象上的另一点,其纵坐标yP>3,求点P到直线A1A2距离的最小值及取得最小值时点P的坐标.
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
(1)若函数f(x)=
| 3x+a |
| x+b |
(2)设点P(x,y)到直线y=x的距离d=
| |x-y| | ||
|
(3)下述命题“若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明;若不正确,请举一反例.若地方不够,可答在试卷的反面.
分析:(1)由函数f(x)=
图象上有两个关于原点对称的不动点,即x2+(b-3)x-a=0有两个互为相反的根,根据方程的根与系数关系可求a,b的关系
(2)若a=8,b=3可得f(x)=
=x可求A1A2所在 的直线方程为x-y=0,设P(x,y)则由y=
>3可得x<-3,点P到直线A1A2的距离d=
=|
|×
=
(x<-3)=-(x+3)+
+6,利用基本不等式可求d的最小值及取得最小值的P
(3)令g(x)=f(x)-x则由f(x)为奇函数可得g(x)为奇函数,由奇函数的性质可得g(0)=0,当x≠0时,若g(x)=0,则g(-x)=-g(x)=0,从而可得g(x)=0的零点有奇数个即f(x)=x的根有奇数个
| 3x+a |
| x+b |
(2)若a=8,b=3可得f(x)=
| 3x+8 |
| x+3 |
| 3x+8 |
| x+3 |
| |x-y| | ||
|
| x2-8 |
| x+3 |
| 1 | ||
|
|x+3+
| ||
|
| 1 |
| -(x+3) |
(3)令g(x)=f(x)-x则由f(x)为奇函数可得g(x)为奇函数,由奇函数的性质可得g(0)=0,当x≠0时,若g(x)=0,则g(-x)=-g(x)=0,从而可得g(x)=0的零点有奇数个即f(x)=x的根有奇数个
解答:解:(1)函数f(x)=
图象上有两个关于原点对称的不动点,
∴f(x)=x有两个互为相反数的根
即x2+(b-3)x-a=0有两个互为相反的根
∴
∴b=3,a>0
(2)若a=8,b=3则可得f(x)=
=x
∴x=±2
即 A1(2
,2
),A2(-2
,-2
)
∴A1A2所在 的直线方程为x-y=0
设P(x,y)则由y=
>3可得x<-3
点P到直线A1A2的距离d=
=|
|×
=
(x<-3)
=
[-(x+3)+
+6]≥
=4
dmin=4
,此时x+3=
即x=-4,P(-4,4)
(3)令g(x)=f(x)-x则由f(x)为奇函数可得g(x)为奇函数
由奇函数的性质可得g(0)=0
当x≠0时,若g(x)=0,则g(-x)=-g(x)=0
∴g(x)=0的零点有奇数个即f(x)=x的根有奇数个
若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个为真命题
| 3x+a |
| x+b |
∴f(x)=x有两个互为相反数的根
即x2+(b-3)x-a=0有两个互为相反的根
∴
|
∴b=3,a>0
(2)若a=8,b=3则可得f(x)=
| 3x+8 |
| x+3 |
∴x=±2
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴A1A2所在 的直线方程为x-y=0
设P(x,y)则由y=
| 3x+8 |
| x+3 |
点P到直线A1A2的距离d=
| |x-y| | ||
|
| x2-8 |
| x+3 |
| 1 | ||
|
|x+3+
| ||
|
=
| 1 | ||
|
| 1 |
| -(x+3) |
2
| ||||
|
| 2 |
dmin=4
| 2 |
| 1 |
| x+3 |
(3)令g(x)=f(x)-x则由f(x)为奇函数可得g(x)为奇函数
由奇函数的性质可得g(0)=0
当x≠0时,若g(x)=0,则g(-x)=-g(x)=0
∴g(x)=0的零点有奇数个即f(x)=x的根有奇数个
若定义在R上的奇函数f(x)图象上存在有限个不动点,则不动点有奇数个为真命题
点评:本题以新定义为切入点,主要考查了方程的根与系数的关系的应用,点到直线的距离公式的应用,及基本不等式在求解函数最值中的应用及条件的配凑,及奇函数性质等知识的综合应用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
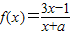 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;