题目内容
记函数f（x）的定义域为D，若存在x0∈D，使得f（x）=x成立，则称（x0，x0）为函数f（x）图象上的“稳定点”.（1）是否存在实数a，使函数f（x）=
的图象上有且仅有两个相异的稳定点?若存在，求出范围；若不存在，请说明理由.
（2）若函数f（x）是定义在R上的奇函数，求证：函数必有奇数个稳定点.
（1）解：设函数f（x）=的图象上有且仅有两个相异的稳定点，则f（x）=
=x，即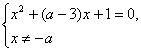
有两个相异的根，
所以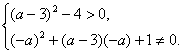
解之，得a＞5或a＜1，a≠-
.
因此存在a∈（-∞，-
）∪（-
，1）∪（5，+∞）使得函数f（x）=
的图象上有且仅有两个相异的稳定点.
（2）证明：因为函数f（x）是定义在R上的奇函数，所以f（-0）=-f（0），即f（0）=0.因此（0，0）是f（x）的一个稳定点.假设函数还有稳定点（x0，x0），即f（x0）=x0，则必定有f（-x0）=-x0.这说明（-x0，-x0）也是函数的稳定点.
综上所述，奇函数的稳定点除原点外，都是成对出现，因此其稳定点的个数是奇数.
练习册系列答案
相关题目
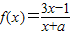的图象上有且只有两个相异的“稳定点”，试求实数a的取值范围；