题目内容
记有限集合A的元素个数为n(A),那么有n(A∪B)=n(A)+n(B)-n(A∩B);n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C).解下列题目:一次会议有1990位数学家参加,每人至少有1327位合作者,求证:可以找到千位数学家,他们中每两个人都合作过.
答案:
解析:
提示:
解析:
|
解:记数学家们为Vi(i=1,2,3,…,1990),与Vi合作过的数学家组成集合Ai,任取合作过的两位数学家记为V1,V2,则n(A1)≥1327,n(A1)≥1327,n(A1∪A2)≤1990,得n(A1∩A2)=n(A1)+n(A2)-n(A1∪A2)≥1327×2-1990>0,从而存在数学家V3∈A1∩A2,V3≠V1,V3≠V2 又∵n(A1∩A2∩A3)=n(A1∩A2)+n(A3)-n[(A1∩A2)∪A3]≥[(1327×2)-1990]+1327-1990=1 ∴存在数学家V4∈A1∩A2∩A3,V4≠V1,V4≠V2,V4≠V3 ∴数学家V1,V2,V3,V4两两合作过. 从而问题得证. 思想方法小结:本题实质是证明A1∩A2∩A3≠φ. |
提示:
|
将实际问题,转化为数学问题,利用集合思想加以解决,充分利用上面两个集合元素个数的公式. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

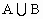 )=card(A)+card(B)-card(
)=card(A)+card(B)-card(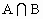 ).
).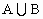 )=card(A)
)=card(A)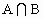 ).
).