题目内容
11.若实数x,y满足不等式组$\left\{\begin{array}{l}x-2≤0\\ y-1≤0\\ x+2y-2≥0\end{array}\right.$,则目标函数z=x-2y的最大值为2.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x-2≤0\\ y-1≤0\\ x+2y-2≥0\end{array}\right.$,作出可行域如图,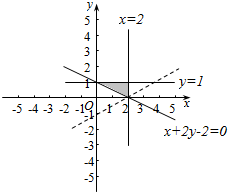
化目标函数z=x-2y为y=$\frac{1}{2}$x-$\frac{z}{2}$,
由图可知,当直线y=$\frac{1}{2}$x-$\frac{z}{2}$过C(2,0)时,直线在y轴上的截距直线,z最大.
∴z=2-2×0=2.
故答案为:2.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
2.打鼾不仅影响别人休息,而且可能与患某种疾病有关.表是一次调查所得的数据,
(1)将本题的2*2联表格补充完整.
(2)用提示的公式计算,每一晚都打鼾与患心脏病有关吗?
提示
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(1)将本题的2*2联表格补充完整.
(2)用提示的公式计算,每一晚都打鼾与患心脏病有关吗?
提示
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| 患心脏病 | 未患心脏病 | 合计 | |
| 每一晚都打鼾 | 3 | 17 | a= |
| 不打鼾 | 2 | 128 | b= |
| 合计 | c= | d= | n= |
6.设集合A={1,2,4,6,8},B={1,2,3,5,6,7},则A∩B的子集个数为( )
| A. | 3 | B. | 6 | C. | 8 | D. | 16 |
16.下列函数中,既是奇函数又是减函数的是( )
| A. | $y=\frac{1}{x}$ | B. | y=-tanx | C. | $y=\frac{{1-{2^x}}}{{1+{2^x}}}$ | D. | y=-x3(-1<x≤1) |
3.已知ABCD是平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D的坐标为( )
| A. | (1,1,-7) | B. | (5,13,-3) | C. | (-3,1,5) | D. | (5,3,1) |