题目内容
1．已知函数f（x）=ax2+bx+1是定义在[a+1，2a]上的偶函数，那么a+b的值为（ ）| A． | $-\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $-\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 依照偶函数的定义，对定义域内的任意实数，f（-x）=f（x），且定义域关于原点对称，a+1=-2a．
解答 解：∵f（x）=ax2+bx+1是定义在[a+1，2a]上的偶函数，
∴f（-x）=f（x），∴b=0，
又a+1=-2a，
∴a=-$\frac{1}{3}$，
∴a+b=-$\frac{1}{3}$．
故选：A．
点评 本题考查偶函数的定义，对定义域内的任意实数，f（-x）=f（x）；奇函数和偶函数的定义域必然关于原点对称，定义域区间2个端点互为相反数．
练习册系列答案
相关题目
12．已知α，β是平面，m，n是直线．下列命题中不正确的是（ ）
| A． | 若m∥n，m⊥α，则n⊥α | B． | 若m∥α，α∩β=n，则m∥n | ||
| C． | 若m⊥α，m⊥β，则α∥β | D． | 若m⊥α，m∩β，则α⊥β |
9．已知在等差数列{an}满足：a11-a4=4，a3+a7-a10=0，记Sn=a1+a2+…+an，则S13=（ ）
| A． | 78 | B． | 68 | C． | 56 | D． | 52 |
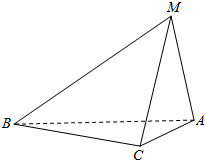如图，在直角三角形BMC中，∠BCM=90°，∠MBC=60°，BM=5，MA=3，且MA⊥AC，AB=4．求MC与平面ABC所成角的正弦值．
10．已知函数f（x）在R上单调递增，且函数f（x-1）是定义在R上的奇函数，则不等式f（x+3）＜0的解集为（ ）
| A． | （-∞，-3） | B． | （4，+∞） | C． | （-∞，1） | D． | （-∞，-4） |