题目内容
A(不等式选做题)若x>0,y>0且x+2y=1,则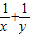 的取值范围是 .
的取值范围是 .B(几何证明选讲选做题)如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则线段DO的长等于 .
C(坐标系与参数方程选做题)曲线
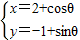 (θ为参数)上一点P,过点A(-2,0) B(0,2)的直线记为L,则点P到直线L距离的最小值为 .
(θ为参数)上一点P,过点A(-2,0) B(0,2)的直线记为L,则点P到直线L距离的最小值为 .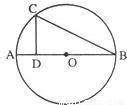
【答案】分析:A根据x>0,y>0且x+2y=1,则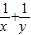 =(
=(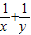 )(x+2y),然后化简整理,最后利用均值不等式即可求出所求.
)(x+2y),然后化简整理,最后利用均值不等式即可求出所求.
B根据直角三角形中的射影定理可知CD2=AD•BD,求出AD,从而求出DO;
C先根据sin2θ+cos2θ=1将参数θ消去,得到曲线方程,再求出直线L的方程,利用点到直线的距离公式求出圆心到直线的距离,即可求出所求.
解答:解:A、∵x>0,y>0且x+2y=1,
∴(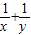 )(x+2y)=3+
)(x+2y)=3+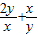 ≥3+2
≥3+2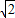
∴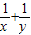 的取值范围是[3+2
的取值范围是[3+2 ,+∞)
,+∞)
故答案为:[3+2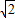 ,+∞)
,+∞)
B、∵∠ACB=90°,CD⊥AB∴CD2=AD•BD即16=AD×8
∴AD=2,则AB=10,OB=5,DO=8-5=3
故答案为:3
C、∵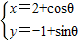 (θ为参数)
(θ为参数)
∴(x-2)2+(y+1)2=1
过点A(-2,0) B(0,2)的直线记为L的方程为x-y+2=0
圆心到直线的距离为d=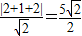
∴点P到直线L距离的最小值为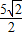 -1
-1
故答案为: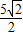 -1
-1
点评:本题主要考查了均值不等式的应用,点到直线的距离公式和参数方程化成普通方程,同时考查了计算能力,属于基础题.
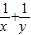 =(
=(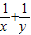 )(x+2y),然后化简整理,最后利用均值不等式即可求出所求.
)(x+2y),然后化简整理,最后利用均值不等式即可求出所求.B根据直角三角形中的射影定理可知CD2=AD•BD,求出AD,从而求出DO;
C先根据sin2θ+cos2θ=1将参数θ消去,得到曲线方程,再求出直线L的方程,利用点到直线的距离公式求出圆心到直线的距离,即可求出所求.
解答:解:A、∵x>0,y>0且x+2y=1,
∴(
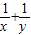 )(x+2y)=3+
)(x+2y)=3+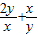 ≥3+2
≥3+2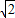
∴
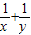 的取值范围是[3+2
的取值范围是[3+2 ,+∞)
,+∞)故答案为:[3+2
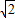 ,+∞)
,+∞)B、∵∠ACB=90°,CD⊥AB∴CD2=AD•BD即16=AD×8
∴AD=2,则AB=10,OB=5,DO=8-5=3
故答案为:3
C、∵
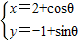 (θ为参数)
(θ为参数)∴(x-2)2+(y+1)2=1
过点A(-2,0) B(0,2)的直线记为L的方程为x-y+2=0
圆心到直线的距离为d=
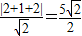
∴点P到直线L距离的最小值为
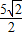 -1
-1故答案为:
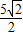 -1
-1点评:本题主要考查了均值不等式的应用,点到直线的距离公式和参数方程化成普通方程,同时考查了计算能力,属于基础题.

练习册系列答案
相关题目
 A(不等式选做题)若x>0,y>0且x+2y=1,则
A(不等式选做题)若x>0,y>0且x+2y=1,则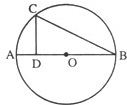 A(不等式选做题)若x>0,y>0且x+2y=1,则
A(不等式选做题)若x>0,y>0且x+2y=1,则 的取值范围是________.
的取值范围是________.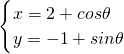 (θ为参数)上一点P,过点A(-2,0) B(0,2)的直线记为L,则点P到直线L距离的最小值为________.
(θ为参数)上一点P,过点A(-2,0) B(0,2)的直线记为L,则点P到直线L距离的最小值为________.