题目内容
（不等式选做题）
若不存在实数x使|x-3|+|x-1|≤a成立，则实数a的取值集合是
若不存在实数x使|x-3|+|x-1|≤a成立，则实数a的取值集合是
{a|a＜2}
{a|a＜2}
．分析：根据绝对值的几何意义得y=|x-3|+|x-1|的几何意义是数轴上点x到点3和1的距离和，由此可得|x-3|+|x-1|的最小值为2．再由题意不存在实数x使|x-3|+|x-1|≤a成立，可知|x-3|+|x-1|的最小值大于a，由此即可得到实数a的取值集合．
解答：解：∵设y=|x-3|+|x-1|，此函数的几何意义是数轴上的点x到点3和1的距离之和，
∴当1≤x≤3时，y=|x-3|+|x-1|达到最小值，最小值为2．
∵不存在实数x使|x-3|+|x-1|≤a成立，
∴y=|x-3|+|x-1|的最小值要大于a，故2＞a，
得实数a的取值集合是{a|a＜2}．
故答案为：{a|a＜2}
∴当1≤x≤3时，y=|x-3|+|x-1|达到最小值，最小值为2．
∵不存在实数x使|x-3|+|x-1|≤a成立，
∴y=|x-3|+|x-1|的最小值要大于a，故2＞a，
得实数a的取值集合是{a|a＜2}．
故答案为：{a|a＜2}
点评：本题给出含有绝对值的不等式，在不等式解集为空集的情况下求参数a的取值集合．着重考查了绝对值的几何意义、不等式的性质和函数最值的求法等知识，属于中档题．
练习册系列答案
相关题目
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.
使
成立，则实数
的取值集合是__________．
，则线段CD的长为________．
：
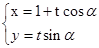（t为参数）与圆C2：
（
为参数）的位置关系不可能是________.