题目内容
【题目】在平面直角坐标系xOy中,点B与点A(﹣1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
【答案】
(1)解:因为点B与A(﹣1,1)关于原点O对称,所以点B得坐标为(1,﹣1).
设点P的坐标为(x,y)
![]()
化简得x2+3y2=4(x≠±1).
故动点P轨迹方程为x2+3y2=4(x≠±1)
(2)解:若存在点P使得△PAB与△PMN的面积相等,设点P的坐标为(x0,y0)
则 ![]() .
.
因为sin∠APB=sin∠MPN,
所以 ![]()
所以 ![]() =
= ![]()
即(3﹣x0)2=|x02﹣1|,解得 ![]()
因为x02+3y02=4,所以 ![]()
故存在点P使得△PAB与△PMN的面积相等,此时点P的坐标为( ![]() )
)
【解析】(1)设点P的坐标为(x,y),先分别求出直线AP与BP的斜率,再利用直线AP与BP的斜率之间的关系即可得到关系式,化简后即为动点P的轨迹方程;(2)对于存在性问题可先假设存在,由面积公式得: ![]() .根据角相等消去三角函数得比例式,最后得到关于点P的纵坐标的方程,解之即得.
.根据角相等消去三角函数得比例式,最后得到关于点P的纵坐标的方程,解之即得.
【考点精析】掌握点到直线的距离公式是解答本题的根本,需要知道点![]() 到直线
到直线![]() 的距离为:
的距离为: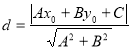 .
.

练习册系列答案
相关题目

