题目内容
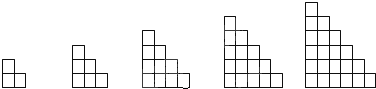
观察下列的图形中小正方形的个数,则第6个图中有
分析:通过观察前几个图形中小正方形的个数得,每一个图形中的小正方形个数都可以看成是一个等差数列的前几项的和,再利用等差数列的求和公式即可解决问题.
解答:解:根据规律性知:
第6个图形中有:1+2+3+4+5+6+7=
=28.
第n个图形中有:1+2+…+(n+1)=
.
故答案为:28;
.
第6个图形中有:1+2+3+4+5+6+7=
| 7(7+1) |
| 2 |
第n个图形中有:1+2+…+(n+1)=
| (n+1)(n+2) |
| 2 |
故答案为:28;
| (n+1)(n+2) |
| 2 |
点评:本题主要考查了归纳推理,以及数列递推式的利用,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目