题目内容
观察下列的图形中小正方形的个数,则第n个图中有
个小正方形.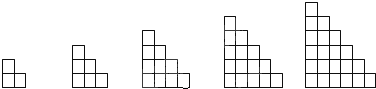
| (n+2)(n+1) |
| 2 |
| (n+2)(n+1) |
| 2 |

分析:由题意可得,f(1)=2+1,f(2)=3+2+1,f(3)=4+3+2+1,f(4)=5+4+3+2+1,f(5)=6+5+4+3+2+1,从而可得f(n),结合等差数列的求和公式可得.
解答:解:由题意可得,f(1)=2+1
f(2)=3+2+1
f(3)=4+3+2+1
f(4)=5+4+3+2+1
f(5)=6+5+4+3+2+1
…
f(n)=(n+1)+n+(n-1)+…+1=
.
故答案为:
.
f(2)=3+2+1
f(3)=4+3+2+1
f(4)=5+4+3+2+1
f(5)=6+5+4+3+2+1
…
f(n)=(n+1)+n+(n-1)+…+1=
| (n+2)(n+1) |
| 2 |
故答案为:
| (n+2)(n+1) |
| 2 |
点评:本题主要考查了等差数列的求和公式在实际问题中的应用,解题的关键是要根据前几个图形的规律归纳出f(n)的代数式,考查了归纳推理的能力.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目



