题目内容
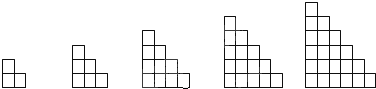
观察下列的图形中小正方形的个数,猜测第n个图中有
个小正方形.

| n(n+1) |
| 2 |
| n(n+1) |
| 2 |

分析:设第n个图形中小正方形的个数为f(n).由题意可得,f(1)=1,f(2)=2+1,f(3)=3+2+1,f(4)=4+3+2+1,f(5)=5+4+3+2+1,f(6)=6+5+4+3+2+1,从而可得f(n),结合等差数列的求和公式可得
解答:解:设第n个图形中小正方形的个数为f(n).
由题意可得,f(1)=1,
f(2)=2+1
f(3)=3+2+1
f(4)=4+3+2+1
f(5)=5+4+3+2+1
f(6)=6+5+4+3+2+1
…
f(n)=n+(n-1)+…+1=
.
故答案为:
.
由题意可得,f(1)=1,
f(2)=2+1
f(3)=3+2+1
f(4)=4+3+2+1
f(5)=5+4+3+2+1
f(6)=6+5+4+3+2+1
…
f(n)=n+(n-1)+…+1=
| n(n+1) |
| 2 |
故答案为:
| n(n+1) |
| 2 |
点评:本题主要考查了归纳推理,以及等差数列的求和公式的应用,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目