题目内容
【题目】数列{an}的前n项和为Sn , Sn=(2n﹣1)an , 且a1=1.
(1)求数列{an}的通项公式;
(2)若bn=nan , 求数列{bn}的前n项和Tn .
【答案】
(1)解:由 ![]() ,可得
,可得 ![]() (n≥2),
(n≥2),
两式相减,得 ![]() ,
,
![]() ,即
,即 ![]() ,
,
故{an}是一个以1为首项, ![]() 为公比的等比数列,
为公比的等比数列,
所以 ![]() ,n∈N*;
,n∈N*;
(2)bn=nan=n( ![]() )n﹣1.
)n﹣1.
Tn=b1+b2+b3++bn= ![]() ,①
,①
![]() =
= ![]() ,②
,②
①﹣②,得 ![]() ,
,
所以 ![]() .
.
【解析】(1.)将n换为n﹣1,两式相减,可得{an}是一个以1为首项, ![]() 为公比的等比数列,运用等比数列的通项公式即可得到;
为公比的等比数列,运用等比数列的通项公式即可得到;
(2.)求得bn=nan=n( ![]() )n﹣1.再由数列的求和方法:错位相减法,结合等比数列的求和公式即可得到所求和.
)n﹣1.再由数列的求和方法:错位相减法,结合等比数列的求和公式即可得到所求和.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系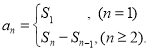 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米. 
(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?


