题目内容
已知椭圆的方程为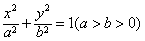 ,它的一个焦点与抛物线y2=8x的焦点重合,离心率e=
,它的一个焦点与抛物线y2=8x的焦点重合,离心率e=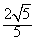 ,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,
,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,
(1)求椭圆的标准方程;
(2)设点M(1,0),且 ,求直线l的方程。
,求直线l的方程。
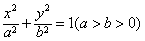 ,它的一个焦点与抛物线y2=8x的焦点重合,离心率e=
,它的一个焦点与抛物线y2=8x的焦点重合,离心率e=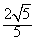 ,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,
,过椭圆的右焦点F作与坐标轴不垂直的直线l,交椭圆于A、B两点,(1)求椭圆的标准方程;
(2)设点M(1,0),且
 ,求直线l的方程。
,求直线l的方程。 解:(1)设椭圆的右焦点为(c,0),
因为y2=8x的焦点坐标为(2,0),所以c=2,
因为 ,所以
,所以 ,
,
故椭圆方程为: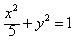 。
。
(2)由(1)得F(2,0),设l的方程为y=k(x-2)(k≠0),
代入 得
得 ,
,
设 ,则
,则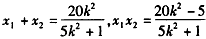 ,
,
∴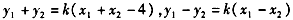 ,
,
∴
 ,
, ,
,
∵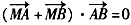 ,
,
∴
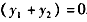 ,
,
∴ ,∴
,∴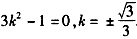 ,
,
所以直线l的方程为 或
或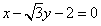 。
。
因为y2=8x的焦点坐标为(2,0),所以c=2,
因为
 ,所以
,所以 ,
,故椭圆方程为:
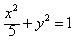 。
。(2)由(1)得F(2,0),设l的方程为y=k(x-2)(k≠0),
代入
 得
得 ,
,设
 ,则
,则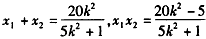 ,
,∴
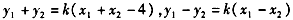 ,
,∴

 ,
, ,
,∵
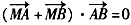 ,
,∴

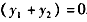 ,
,∴
 ,∴
,∴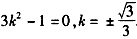 ,
,所以直线l的方程为
 或
或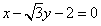 。
。 
练习册系列答案
相关题目
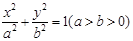 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,离心率
的焦点重合,离心率 ,过椭圆的右焦点
,过椭圆的右焦点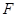 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、 两点.
两点. ,且
,且 ,求直线
,求直线 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,离心率
的焦点重合,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、 两点.(Ⅰ)求椭圆的标准方程; (Ⅱ)设点
两点.(Ⅰ)求椭圆的标准方程; (Ⅱ)设点 ,且
,且 ,求直线
,求直线 ,它的一个焦点与抛物线
,它的一个焦点与抛物线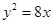 的焦点重合,离心率
的焦点重合,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、 两点.
两点. ,且
,且 ,求直线
,求直线 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,离心率
的焦点重合,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于 、
、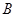 两点.
两点. ,且
,且 ,求直线
,求直线 ,它的两个焦点为F1、F2,若| F1F2|=8, 弦AB过F1 ,则△ABF2的周长为 ▲
,它的两个焦点为F1、F2,若| F1F2|=8, 弦AB过F1 ,则△ABF2的周长为 ▲