题目内容
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度。已知直线经过点P(1,1),倾斜角α=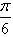 ;
;
(1)写出直线l参数方程;
(2)设l与圆ρ=2相交于两点A、B,求点P到A、B两点的距离之积。
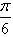 ;
;(1)写出直线l参数方程;
(2)设l与圆ρ=2相交于两点A、B,求点P到A、B两点的距离之积。
解:(1)直线的参数方程是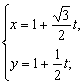 (t是参数);
(t是参数);
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1,t2
则点A,B的坐标分别为

圆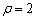 化为直角坐标系的方程
化为直角坐标系的方程
以直线l的参数方程代入圆的方程 整理得
整理得 ①
①
因为 是方程①的解,从而
是方程①的解,从而 =-2
=-2
所以|PA|·|PB|= =|-2|=2。
=|-2|=2。
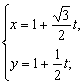 (t是参数);
(t是参数);(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1,t2
则点A,B的坐标分别为


圆
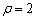 化为直角坐标系的方程
化为直角坐标系的方程
以直线l的参数方程代入圆的方程
 整理得
整理得 ①
①因为
 是方程①的解,从而
是方程①的解,从而 =-2
=-2所以|PA|·|PB|=
 =|-2|=2。
=|-2|=2。
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目