题目内容
已知O为坐标原点，M(cosx，2| 3 |
| ||
| 6 |
x∈R，a为常数，设函数f(x)=
| OM |
| ON |
（1）求函数y=f（x）的表达式和最小正周期；
（2）若角C为△ABC的三个内角中的最大角且y=f（C）的最小值为0，求a的值；
（3）在（2）的条件下，试画出y=f（x）（x∈[0，π]）的简图．
分析：（1）根据向量数量积的坐标表示和两角和的正弦公式，求出函数的解析式并进行化简，利用周期公式求出函数的最小正周期；
（2）根据三角形最大角的范围求出2C+
的范围，再由正弦函数的性质以及最小值求出a的值；
（3）根据（2）求出的函数解析式，以及对应坐标系中的标出的自变量的值求出对应的函数值，利用描点连线和正弦曲线，画出函数的简图．
（2）根据三角形最大角的范围求出2C+
| π |
| 6 |
（3）根据（2）求出的函数解析式，以及对应坐标系中的标出的自变量的值求出对应的函数值，利用描点连线和正弦曲线，画出函数的简图．
解答：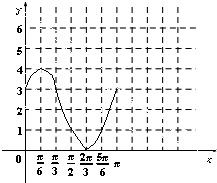
解：（1）由题意知，f(x)=
•
则f(x)=2cos2x+2
(sinxcosx+
a)=cos2x+
sin2x+1+a
=2sin(2x+
)+a+1
∴T=π
（2）由角C为△ABC的三个内角中的最大角可得：
≤C＜π，2C+
∈[
π，
π)，
∴y=f(C)=2sin(2C+
)+a+1的最小值为2×（-1）+a+1=0，
则a=1．
（3）由（2）可知：y=f(x)=2sin(2x+
)+2，
依次求出f（0）=3，f（
）=4，f（
）=3，f（
）=1，f（
）=0，f（
）=1，f（π）=3．
在坐标系中进行描点连线，画出函数的图象（x∈[0，π]）：
解：（1）由题意知，f(x)=| OM |
| ON |
则f(x)=2cos2x+2
| 3 |
| ||
| 6 |
| 3 |
=2sin(2x+
| π |
| 6 |
∴T=π
（2）由角C为△ABC的三个内角中的最大角可得：
| π |
| 3 |
| π |
| 6 |
| 5 |
| 6 |
| 13 |
| 6 |
∴y=f(C)=2sin(2C+
| π |
| 6 |
则a=1．
（3）由（2）可知：y=f(x)=2sin(2x+
| π |
| 6 |
依次求出f（0）=3，f（
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
| 5π |
| 6 |
在坐标系中进行描点连线，画出函数的图象（x∈[0，π]）：
点评：本题是向量和三角函数的综合题，考查了向量数量积的坐标表示和正弦函数的性质应用，综合运用知识和作图能力．
练习册系列答案
相关题目
已知O为坐标原点，
），N（2cosx，sinxcosx+
a），其中x∈R，a为常数，设函数
，